
如图1至图4中,两平行线AB、CD间的距离均为6,点M为AB上一定点.
思考:如图1,圆心为0的半圆形纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α。
当α=__ __度时,点P到CD的距离最小,最小值为__  __.
__.
探究一:在图1的基础上,以点M为旋转中心,在AB,CD 之间顺时针旋转该半圆形纸片,直到不能再转动为止,如图2,得到最大旋转角∠BMO=_ __度,此时点N到C D的距离是__ __.
D的距离是__ __.
探究二:将如图1中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转。
(1)如图3,当α=60°时,求 在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
(2)如图4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请直接确定α的最大值=__ __.

科目:初中数学 来源: 题型:
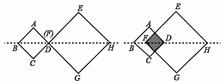
如图,四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H方向平移至点B与点H重合时停止,设点D、F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与 x之间函数关系的图象是( )
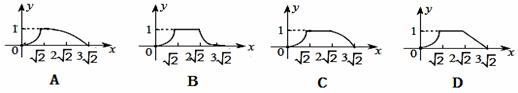
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题正确的是 ( )
A.三点可以确定一个圆; B.以定点为圆心, 定长为半径可确定一个圆;
C.顶点在圆上的三角形叫圆的外接三角形; D.等腰三角形的外心一定在这个三角形内.
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线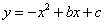 上部分点的横坐标
上部分点的横坐标 ,纵坐标
,纵坐标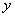 的对应值如下表:
的对应值如下表:
|
| … |
|
| 0 | 1 | 2 | … |
|
| … | 0 | 4 | 6 | 6 | 4 | … |
由上表可知,下列说法正确的个数是 ( )
①抛物线与 轴的一个交点为
轴的一个交点为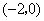 ②抛物线与
②抛物线与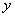 轴的交点为
轴的交点为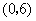
③抛物线的对称轴是: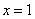 ④在对称轴左侧
④在对称轴左侧 随
随 增大而增大
增大而增大
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com