
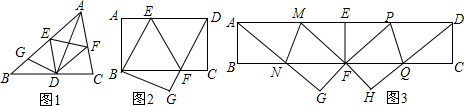
���� ��1���ȸ��������۵����ó���AEFΪ���������Σ��ٸ���EF��ֱƽ��AD���ó�AE=DE��AF=DF�����ɵ��ı���AEDF���ı���ȣ��ɴ˿��ж��ı���AEDF�����Σ�
��2���ȸ����۵������ʵó�DE=BE��DF=BF���ٸ��ݵȽǶԵȱߵó�DE=DF�������ݡ���������ȵ��ı���Ϊ���Ρ��ж��ı���BEDF�����Σ�
��3�����ȸ���ֱ�������ε�������ǻ�����á�EMF���ٸ����۵���á�NMF�Ķ�����������ƽ���ߵ�������á�MNG�Ķ�������������AF���������ε������Լ����������ε����ʣ��ж�Rt��MGF��Rt��MEF���ٸ��ݡ�MAG=��MFG=��MFE����á�EAF=30�㣬������EF��AE��������ϵ�õ�AB��AD��������ϵ��
���  �⣺��1���ı���AEDF�����Σ�
�⣺��1���ı���AEDF�����Σ�
֤������ͼ1����AD��EF���ڵ�G��
�ɵ�һ���۵��ã���BAD=��CAD��
�ɵڶ����۵��ã�AD��EF��ֱƽ�֣�
���AGE=��AGF=90�㣬
���AEF=��AFE��
��AE=AF������AEF����������
��EF��ֱƽ��AD��
��AE=DE��AF=DF��
��AE=DE=AF=DF��
���ı���AEDF�����Σ�
�ʴ�Ϊ�����Σ�
��2���ı���BEDF�����Σ�
���ɣ� ��ͼ2������BD�����۵������ʿ�֪��BD��EF��ֱƽ�֣�
��ͼ2������BD�����۵������ʿ�֪��BD��EF��ֱƽ�֣�
��DE=BE��DF=BF��
���ı���ABCD�Ǿ��Σ�
��AD��BC��
���BFE=��DEF��
���۵��ã���BFE=��DFE
���DEF=��DFE��
��DE=DF��
��DE=BE=DF=BF��
���ı���BEDF�����Σ�
��3������ͼ3������MFE=40�㣬���۵���֪����EMF=90��-40��=50�㣬
���NMF=��180��-50�㣩��$\frac{1}{2}$=65�㣬
��MF��NG��
���MNG=180��-��NMF=115�㣻
�ھ��γ�AD���AB��������ϵΪ��AD=2$\sqrt{3}$AB
���ɣ�����AF��������ANFM�У�MG��FG����MAG=��MFG��MG=$\frac{1}{2}$MN��
���۵��ɵã�MF=PF��EF��MP
��ME=$\frac{1}{2}$MP
��MG=ME
��Rt��MGF��Rt��MEF��
$\left\{\begin{array}{l}{MG=ME}\\{MF=MF}\end{array}\right.$
��Rt��MGF��Rt��MEF��HL��
���MFG=��MFE
���MAG=��MFG=��MFE
�֡ߡ�MAG+��MFG+��MFE=90��
���MAG=��MFG=��MFE=30��
��ֱ��������AEF�У�$\frac{EF}{AE}$=$\frac{1}{\sqrt{3}}$����$\frac{EF}{AD}$=$\frac{1}{2\sqrt{3}}$
��EF=AB
��$\frac{AB}{AD}$=$\frac{1}{2\sqrt{3}}$
�����γ�AD���AB��������ϵΪ��AD=2$\sqrt{3}$AB
���� �������۵�Ϊ������������ԳƵ������Լ����ε��ж������ʣ��������Ĺؼ����������ε��ж�����������ʱע�⣺�۵�������ı�������Գ����ʵ����ã�����ʱҪץס����Ӧ����ȣ���Ӧ�߶���ȡ���Щ������ϵ��


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֱ��ǽ��AOB��OA��OB����OA��OB���Ȳ��ޣ��У�Ҫ��20m����ǽ����ֱ��ǽ��AOBΧ�ɵ���Ϊ���εĴ��֣��ҵ������AOBC�����Ϊ96m2��
��ֱ��ǽ��AOB��OA��OB����OA��OB���Ȳ��ޣ��У�Ҫ��20m����ǽ����ֱ��ǽ��AOBΧ�ɵ���Ϊ���εĴ��֣��ҵ������AOBC�����Ϊ96m2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�����������y=$\frac{m}{x}$��ͼ����һ�κ���y=k��x-2����ͼ��ΪA��3��2����B��x��y����
��ͼ����ƽ��ֱ������ϵxOy�У�����������y=$\frac{m}{x}$��ͼ����һ�κ���y=k��x-2����ͼ��ΪA��3��2����B��x��y�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��a+b����a-b�� | B�� | b��a-b��2 | C�� | b��a2-b2�� | D�� | b��a+b��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ȼ� | �ɼ�����m��ʾ�� | Ƶ�� | Ƶ�� |
| A | 90��m��100 | x | 0.08 |
| B | 80��m��90 | 34 | y |
| C | m��80 | 12 | 0.24 |
| �ϼ� | 50 | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 52017-1 | B�� | 52016-1 | C�� | $\frac{{5}^{2017}-1}{4}$ | D�� | $\frac{{5}^{2016}-1}{4}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com