
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )

A.(4n﹣1,![]() ) B.(2n﹣1,
) B.(2n﹣1,![]() ) C.(4n+1,
) C.(4n+1,![]() ) D.(2n+1,
) D.(2n+1,![]() )
)
【答案】C.
【解析】
试题分析:∵△OA1B1是边长为2的等边三角形,∴A1的坐标为(1,![]() ),B1的坐标为(2,0),∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∵2×2﹣1=3,2×0
),B1的坐标为(2,0),∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∵2×2﹣1=3,2×0![]() =
=![]() ,∴点A2的坐标是(3,
,∴点A2的坐标是(3,![]() ),
),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,∴点A3与点A2关于点B2成中心对称,∵2×4﹣3=5,2×0﹣(![]() )=
)=![]() ,∴点A3的坐标是(5,
,∴点A3的坐标是(5,![]() ),
),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,∴点A4与点A3关于点B3成中心对称,∵2×6﹣5=7,2×0![]() =
=![]() ,∴点A4的坐标是(7,
,∴点A4的坐标是(7,![]() ),
),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是![]() ,当n为偶数时,An的纵坐标是
,当n为偶数时,An的纵坐标是![]() ,∴顶点A2n+1的纵坐标是
,∴顶点A2n+1的纵坐标是![]() ,
,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,![]() ).故选C.
).故选C.


科目:初中数学 来源: 题型:
【题目】小聪与同桌小明在课下学习中遇到这样一道数学题:“如图(1),在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试确定线段AE与DB的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答: 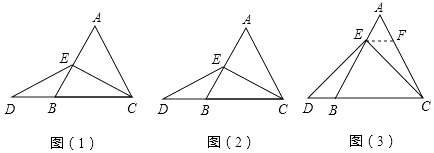
(1)取特殊情况,探索讨论: 当点E为AB的中点时,如图(2),确定线段AE与DB的大小关系,请你写出结论:AEDB(填“>”,“<”或“=”),并说明理由.
(2)特例启发,解答题目: 解:题目中,AE与DB的大小关系是:AEDB(填“>”,“<”或“=”).理由如下:如图(3),过点E作EF∥BC,交AC于点F.(请你将剩余的解答过程完成)
(3)拓展结论,设计新题: 在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若△ABC的边长为1,AE=2,则CD的长为 . (请你画出图形,并直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系内画一次函数y1=﹣x+4和y2=2x﹣5的图象,根据图象求:
(1)方程﹣x+4=2x﹣5的解;
(2)当x取何值时,y1>y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A2处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015,到BC的距离记为h2015.若h1=1,则h2015的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将方程x(x﹣3)+1=0化为一元二次方程的一般形式是( )
A.x2﹣3x+1=0B.x2+3x+1=0
C.x2﹣3x﹣1=0D.x2+x﹣3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD与CE相交于点O,AD=AE,∠B=∠C,请解答下列问题:
(1)△ABD与△ACE全等吗?为什么?
(2)BO与CO相等吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com