
 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.分析 (1)由|2a+b+1|+(a+2b-4)2=0根据非负数性质可得关于a、b的方程组,解方程组可得;
(2)根据A、B、C三点坐标求出$\frac{1}{3}$S△ABC,设点M(x,0),由S△COM=$\frac{1}{3}$S△ABC列出方程求解可得.
解答 解:(1)∵|2a+b+1|+(a+2b-4)2=0,
∴$\left\{\begin{array}{l}{2a+b+1=0}\\{a+2b-4=0}\end{array}\right.$,
解得:a=-2,b=3;
(2)由(1)知点A(-2,0),B(3,0),C(-1,2),
∴S△ABC=$\frac{1}{2}$×AB×yC=$\frac{1}{2}$×5×2=5,
设点M(x,0),
∵S△COM=$\frac{1}{3}$S△ABC,
∴$\frac{1}{2}$×x×2=$\frac{1}{3}$×5,
解得:x=$\frac{5}{3}$,
故点M的坐标为($\frac{5}{3}$,0).
点评 本题主要考查坐标与图形的性质、非负数性质、解方程组、三角形面积的计算,根据点的坐标表示出线段的长是解题的根本.


科目:初中数学 来源: 题型:解答题
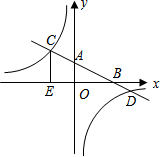 如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
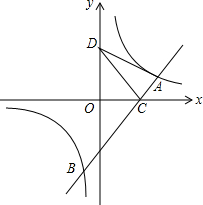 如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC.
如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
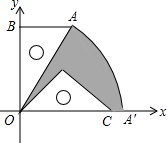 如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)
如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com