
(1)证明:∵AB
2+BD
2=3
2+4
2=5
2=AD
2∴△ABD为直角三角形,且AB⊥BD.
由于x轴⊥y轴,AB在x轴上,且B为原点,因此点D在y轴上.
(2)解:显然,P点坐标为(0,5),且PQ=DC=4,∠QPB=∠DAB.
过Q点作QH⊥BD,垂足为H.
在Rt△PQH中,QH=PQ•sin∠QPH=PQ•sin∠DAB=4×

=

.
PH=PQ•cos∠QPH=PQ•cos∠DAB=4×

=
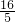
.
BH=PB-PH=5-
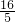
=
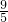
.
∴Q(-

,
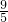
).
∵直线过P、Q两点.
∴

,解得

.
∴直线PQ的解析式为y=

x+5.

(3)解:设B′T′与AB交于点M,Q′T′交AB于点E,交AD于点F.
∵0<m≤3,∴S=S
梯形BDFE-S
△BB′M.
由(2)可知,BE=QH=

.
∴AE=AB-BE=4-

=

.
∴EF=AE•tan∠DAB=

×

=

.
∴S
梯形BDFE=

(EF+BD)•BE=

×(

+3)×

=

.
又ET′∥BB′,∴∠MB′B=∠T′=∠DAB.
∴BM=BB′•tan∠MBB=m•tan∠DAB=

m.
∴S
△BB'M=

BM•BB′=

×

m×m=

m
2.
∴S=

-

m
2(0<m≤3).
分析:(1)根据AB、BD、AD的长,不难得出三角形ABD为直角三角形.由于A、B在x轴上,且B为原点,因此D必在y轴上;
(2)点P的坐标易求出,关键是求出Q点的坐标,可过Q作QH⊥y轴于H,那么可在直角三角形PQH中,根据PQ的长和∠QPB的三角函数值(∠QPB=∠DAB),求出PH,QH的长,即可得出Q点的坐标,然后用待定系数法求出直线PQ的解析式.
(3)当0<m≤3,B'在线段BD上,此时重合部分是个五边形.设TB'与x轴的交点为M,AD与Q'T的交点为F,那么重合部分的面积可用梯形EFDB的面积-三角形EBB'的面积来求得.
梯形的上底可用AE的长和∠DAB的正切值求出(AE的长为A点横坐标绝对值与Q点横坐标绝对值的差),同理可在直角三角形BB′M中求出BM的长,由此可求出S、m的函数关系式.
点评:本题主要考查了勾股定理、平行四边形的性质、图形的翻转变换、图形面积的求法以及一次函数、二次函数的应用等知识点.综合性强,难度较大.


 (1)证明:∵AB2+BD2=32+42=52=AD2
(1)证明:∵AB2+BD2=32+42=52=AD2 =
= .
. =
=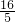 .
.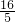 =
=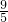 .
. ,
,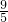 ).
). ,解得
,解得 .
. x+5.
x+5.
 .
. =
= .
. ×
× =
= .
. (EF+BD)•BE=
(EF+BD)•BE= ×(
×( +3)×
+3)× =
= .
. m.
m. BM•BB′=
BM•BB′= ×
× m×m=
m×m= m2.
m2. -
- m2(0<m≤3).
m2(0<m≤3).

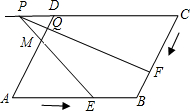 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.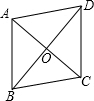 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2