
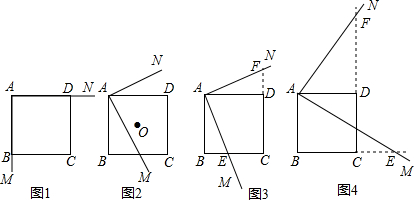

分析 (1)利用勾股定理和正方形的性质得出x2+y2=2即可;
(2)①利用全等三角形的判定和性质证明△ABE与△ADF全等,即可得到BE=DF;
②利用①的结论和三角形面积的关系进行证明即可;
(3)①将△ABG绕点A逆时针旋转90°至△ADQ,证明△QDH与△GAH相似,进而证明即可;
②利用①中结论得出即可.
解答 解:(1)在图中作出正方形的中心O到AM、AN的距离分别记为x、y,如图1: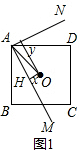
在Rt△AOH中,OA2=x2+y2,
即可得:${x}^{2}+{y}^{2}=(\frac{2\sqrt{2}}{2})^{2}=2$,
故答案为:④;
(2)①∵∠BAE=90°-∠DAM=∠DAF,
∴在△ABE与△ADF中,
$\left\{\begin{array}{l}{∠BAE=∠DAF}\\{AB=AD}\\{∠ABE=∠ADF=90°}\end{array}\right.$,
∴△ABE≌△ADF(ASA),
∴BE=DF;
②同①可证:BE=DF,连接AC,如图2:
S△APF-S△CPE=S△ACF-S△ACE=$\frac{1}{2}$CF•AD-$\frac{1}{2}$CE•AB=CF-CE=CD+DF-(BE-BC)=CD+BC=4;
(3)①将△ABG绕点A逆时针旋转90°至△ADQ,如图3:
∵AB=AD,
∴∠ABG=∠ADQ=45°,
∴∠QDH=90°=∠GAH,
∴△QDH∽△GAH,
∴$\frac{QD}{DH}=\frac{AG}{AH}$,
∵BG=QD,
∴$\frac{BG}{DH}=\frac{AG}{AH}$;
②当45<α<90时,AM、AN的反向延长线与直线BD分别相交于点G,H,①中的结论还成立,理由如下:
将△ABH绕点A逆时针旋转90°至△ADQ,如图4:
∵AB=AD,
∴∠ABG=∠ADQ=45°,
∴∠QDH=90°=∠GAH,
∴△QDH∽△GAH,
∴$\frac{QD}{DH}=\frac{AG}{AH}$,
∵BG=QD,
∴$\frac{BG}{DH}=\frac{AG}{AH}$.
点评 此题考查几何变换问题,关键是根据全等三角形的判定和性质以及相似三角形的判定和性质进行分析解答.


科目:初中数学 来源: 题型:选择题
| A. | 中位数是8 | B. | 众数是9 | C. | 平均数是8 | D. | 方差是1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查我区奶制品中蛋白质含量是否达到国家标准 | |
| B. | 调查我区6月1日这天嘉陵江水中氨氮含量是否超标 | |
| C. | 调查我校初三某班全体学生的视力状况 | |
| D. | 调查我区市民对消防安全知识的知晓情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2.
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com