
 .根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.
.根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.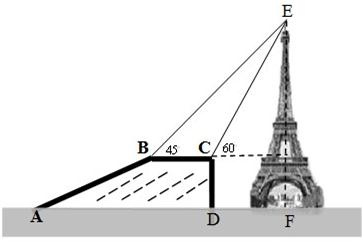
 解:不需测量其它数量就能求出塔高.
解:不需测量其它数量就能求出塔高. ,不妨设BH=k,则AH=
,不妨设BH=k,则AH= k.
k. x.
x. ≈47.3,
≈47.3,

科目:初中数学 来源: 题型:
| 3 |
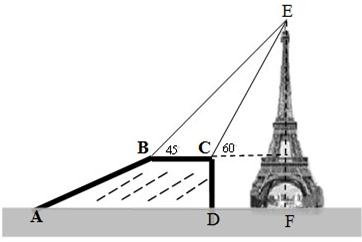
查看答案和解析>>
科目:初中数学 来源: 题型:
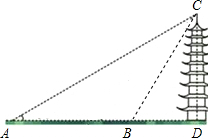 (2013•婺城区二模)小明和小刚在节假日到某风景区游玩,决定用所学知识对景区内的一宝塔进行测量.如图,他们先在A处测得塔顶C的仰角为30°;再向塔的方向直行80米到达B处,又测得塔顶C的仰角为60°.设塔高CD为x米.
(2013•婺城区二模)小明和小刚在节假日到某风景区游玩,决定用所学知识对景区内的一宝塔进行测量.如图,他们先在A处测得塔顶C的仰角为30°;再向塔的方向直行80米到达B处,又测得塔顶C的仰角为60°.设塔高CD为x米.查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市婺城区中考数学二模试卷(解析版) 题型:解答题
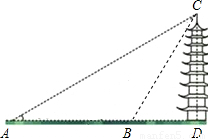 小明和小刚在节假日到某风景区游玩,决定用所学知识对景区内的一宝塔进行测量.如图,他们先在A处测得塔顶C的仰角为30°;再向塔的方向直行80米到达B处,又测得塔顶C的仰角为60°.设塔高CD为x米.
小明和小刚在节假日到某风景区游玩,决定用所学知识对景区内的一宝塔进行测量.如图,他们先在A处测得塔顶C的仰角为30°;再向塔的方向直行80米到达B处,又测得塔顶C的仰角为60°.设塔高CD为x米.查看答案和解析>>
科目:初中数学 来源:2009年上海市青浦区中考数学一模试卷(解析版) 题型:解答题
 .根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.
.根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.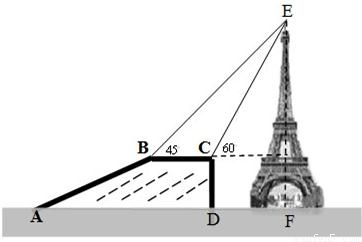
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com