
【题目】已知⊙O与直线l相切于A点,点P、Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动.连接OQ、OP(如图),则阴影部分面积S1、S2的大小关系是( )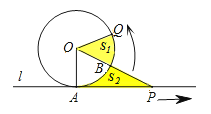
A.S1=S2
B.S1≤S2
C.S1≥S2
D.先S1<S2 , 再S1=S2 , 最后S1>S2
科目:初中数学 来源: 题型:
【题目】一项工程,甲乙两人合作需要8天完成任务,若甲单独做需要12天完成任务.
(1)若甲乙两人一起做6天,剩下的由甲单独做,还需要几天完成?
(2)若甲乙两人一起做4天,剩下的由乙单独做,还需要几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD的周长.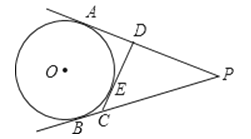
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“微薄问政”当属时下最时髦的词汇之一,今年3月全国人大和政协年度会议期间,不少代表和委员通过微薄与民众进行沟通.3月25日到4月5日,环球舆情调查中心以网络在线调查和电话调查两种方式在北京市就使用微薄动因、关注内容以及“微薄问政”的态度等问题进行了调查, 以下是“微薄问政”的态度的统计图表.
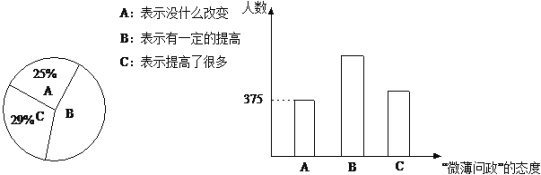
(1)求认为微薄对政治关注的程度有一定提高的人数的百分比;
(2)求在此调查中认为微薄对政治关注的程度提高了很多的人数;
(3)在北京市2500万人口中请你估计一下认为微薄对政治的关注程度没有什么改变的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )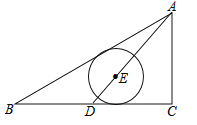
A.![]() ≤R≤
≤R≤![]()
B.![]() ≤R≤
≤R≤![]()
C.![]() ≤R≤2
≤R≤2
D.1≤R≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:正整数n的“H运算”是:①当n为奇数时,H=3n+13;②当n为偶数时,H=n![]() …(连续乘以
…(连续乘以![]() ,一直算到H为奇数止).如:数3经过“H运算”的结果是22,经过2次“H运算”的结果为11,经过三次“H运算”的结果为46,那么257经2017次“H运算”得到的结果是( )
,一直算到H为奇数止).如:数3经过“H运算”的结果是22,经过2次“H运算”的结果为11,经过三次“H运算”的结果为46,那么257经2017次“H运算”得到的结果是( )
A. 161 B. 1 C. 16 D. 以上答案均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
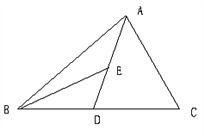
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作图:在△BED中作出BD边上的高EF;BE边上的高DG;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高EF为多少?若BE=6,求△BED中BE边上的高DG为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
A.∠AEB+22°=∠DEF
B.1+tan∠ADB=![]()
C.2BC=5CF
D.4cos∠AGB=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com