
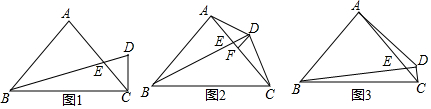
���� ��1����Rt��ABE�У�����AB=3=AC����ABE=30�㣬���AE=$\sqrt{3}$��BE=2$\sqrt{3}$��CE=3-$\sqrt{3}$�����ж���ABE�ס�DCE���õ�$\frac{CD}{BA}$=$\frac{CE}{BE}$���ݴ����CD�ij���
��2���ӳ�CD��BA���ڵ�G�����ж���GBD�ա�CBD��ASA�����õ�D��GC���е㣬���ж���ABE�ա�ACG��ASA�����õ�AE=AG����������������λ�߶������ó�AG=2DF�����ɵõ�AE=2DF��
��3���ӳ�BA��CD���ڵ�M����A��AN��BD��N���ж���BDM�ס�CAM�������õ���ADM�ס�CBM����á�MDA=��ABC=45��=��ADN���ٸ���BD=$\frac{7}{2}$$\sqrt{2}$��AD=3���õ�AN��BN�ij��������ݡ�ABN�ס�ECD���ó�$\frac{ED}{CD}$=$\frac{3}{4}$�����ɵõ�Rt��CDE�д���$\frac{DE+CE}{CD}$=2��
��� 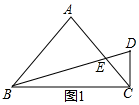 �⣺��1����ͼ1����Rt��ABE�У���AB=3=AC����ABE=30�㣬
�⣺��1����ͼ1����Rt��ABE�У���AB=3=AC����ABE=30�㣬
��AE=$\sqrt{3}$��BE=2$\sqrt{3}$��
��CE=3-$\sqrt{3}$��
��CD��BD����A=90�㣬��AEB=��DEC��
���ABE�ס�DCE��
��$\frac{CD}{BA}$=$\frac{CE}{BE}$����$\frac{CD}{3}$=$\frac{3-\sqrt{3}}{2\sqrt{3}}$��
���CD=$\frac{3\sqrt{3}-3}{2}$��
��2����ͼ2���ӳ�CD��BA���ڵ�G��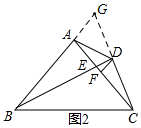
��BDƽ�֡�ABC��CD��BD��
���GBD=��CBD����BDG=��BDC��
�֡�BD=BD��
���GBD�ա�CBD��ASA����
��GD=CD����D��GC���е㣬
��CD��BD����A=90�㣬��AEB=��DEC��
���ABE=��ACG����BAE=��CAG=90�㣬
�֡�AB=AC��
���ABE�ա�ACG��ASA����
��AE=AG��
��F��AC���е㣬D��GC���е㣬
��DF�ǡ�ACG����λ�ߣ�
��AG=2DF��
��AE=2DF��
��3����ͼ3���ӳ�BA��CD���ڵ�M����A��AN��BD��N��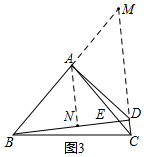
�ߡ�BDM=��CAM=90�㣬��M=��M��
���BDM�ס�CAM��
��$\frac{DM}{AM}$=$\frac{BM}{CM}$����$\frac{DM}{BM}$=$\frac{AM}{CM}$��
�ߡ�M=��M��
���ADM�ס�CBM��
���MDA=��ABC=45��=��ADN��
��AD=3��
�����ֱ��������ADN�У�AN=DN=$\frac{3}{2}\sqrt{2}$��
��BN=$\frac{7}{2}\sqrt{2}$-$\frac{3}{2}\sqrt{2}$=2$\sqrt{2}$��
�ߡ�ABN=��ECD����ANB=��EDC=90�㣬
���ABN�ס�ECD��
��$\frac{AN}{BN}$=$\frac{ED}{CD}$����$\frac{\frac{3}{2}\sqrt{2}}{2\sqrt{2}}$=$\frac{ED}{CD}$��
��$\frac{ED}{CD}$=$\frac{3}{4}$��
��ED=3k��CD=4k����Rt��CDE��CE=5k��
��$\frac{DE+CE}{CD}$=$\frac{3k+5k}{4k}$=2��
���� ���������������ۺ��⣬��Ҫ�����˵���ֱ�������ε����ʣ�ȫ���������ж������ʣ����������ε��ж������ʣ���������λ�߶����Լ����ɶ������ۺ�Ӧ�ã��������Ĺؼ����������߹���ȫ�������κ����������Σ�����ȫ�������εĶ�Ӧ������Լ����������εĶ�Ӧ�߳ɱ���������⣮


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
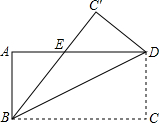 ��ͼ����������ABC���ŶԽ���BD�۵���ʹ��C����C�䴦��BC�佻AD�ڵ�E��
��ͼ����������ABC���ŶԽ���BD�۵���ʹ��C����C�䴦��BC�佻AD�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
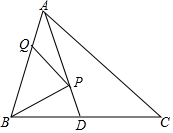 ��֪����ͼ����ABC�У���P��Q�ֱ��ǡ�BAC��ƽ����AD����AB�ϵ��������㣬��C=����BC=6��
��֪����ͼ����ABC�У���P��Q�ֱ��ǡ�BAC��ƽ����AD����AB�ϵ��������㣬��C=����BC=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | �Ǹ��� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
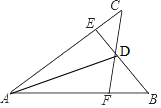 ��ͼ����֪AB=AC��AE=AF��BE��CF���ڵ�D��
��ͼ����֪AB=AC��AE=AF��BE��CF���ڵ�D���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com