
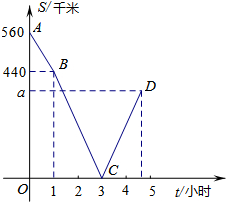
 甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.
甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.分析 (1)根据图象,甲出发时的S值即为M、N两地间的距离;先求出甲车的速度,然后设乙车的速度为xkm/h,再利用相遇问题列出方程求解即可;然后求出相遇后甲车到达N地的时间,再根据路程=速度×时间求出两车的相距距离a即可;
(2)设直线BC的解析式为S=k1t+b1(k1≠0),利用待定系数法求出直线BC的解析式,再令S=330,求出t的值;设直线CD的解析式为S=k2t+b2(k2≠0),利用待定系数法求出直线CD的解析式,再令S=330,求出t的值,进而得出答案.
解答 解:(1)t=0时,S=560,
所以,M、N两地的距离为560千米;
甲车的速度为:(560-440)÷1=120km/h,
设乙车的速度为xkm/h,
则(120+x)×(3-1)=440,
解得x=100;
相遇后甲车到达N地的时间为:(3-1)×100÷120=$\frac{5}{3}$(小时),
所以,a=(120+100)×$\frac{5}{3}$=$\frac{1100}{3}$千米;
故答案为:120,100,$\frac{1100}{3}$;
(2)设直线BC的解析式为S=k1t+b1(k1≠0),
将B(1,440),C(3,0)代入得,
$\left\{\begin{array}{l}{{k}_{1}+{b}_{1}=440}\\{3{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=220}\\{{b}_{1}=660}\end{array}\right.$,
所以,S=-220t+660,
当-220t+660=330时,解得t=1.5,
直线CD的解析式为S=k2t+b2(k2≠0),
点D的横坐标为$\frac{5}{3}$+3=$\frac{14}{3}$,
将C(3,0),D($\frac{14}{3}$,$\frac{1100}{3}$)代入得,$\left\{\begin{array}{l}{3{k}_{2}+{b}_{2}=0}\\{\frac{14}{3}{k}_{2}+{b}_{2}=\frac{1100}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=220}\\{{b}_{2}=-660}\end{array}\right.$,
所以,S=220t-660(3≤t≤$\frac{14}{3}$)
当220t-660=330时,解得t=4.5,
答:甲出发1.5小时或4.5小时后两车相距330千米.
点评 本题考查了一次函数的应用,主要利用了路程、速度、时间三者之间的关系,准确识图并获取信息是解题的关键,(2)要分相遇前和相遇后两种情况讨论.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
 已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).
已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm,8cm,12cm | B. | 3cm,4cm,5cm | ||
| C. | 6cm,9cm,15cm | D. | 100cm,200cm,300cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为( )
如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为( )| A. | 80° | B. | 70° | C. | 90° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )| A. | PC=PD | B. | ∠CPO=∠DOP | C. | ∠CPO=∠DPO | D. | OC=OD |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省揭阳市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
函数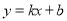 (
(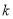 、
、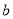 为常数,
为常数,  )图象如图所示,则关于
)图象如图所示,则关于 的不等式
的不等式 的解集为( )
的解集为( )

A.  B.
B. 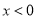 C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com