
 如图,△ABC、△DEF和△GMN都是等边三角形,且点E、M在线段AC上,点G在线段EF上,那么∠1+∠2+∠3等于( )
如图,△ABC、△DEF和△GMN都是等边三角形,且点E、M在线段AC上,点G在线段EF上,那么∠1+∠2+∠3等于( )| A. | 90° | B. | 120° | C. | 150° | D. | 180° |
分析 由等边三角形的性质和平角的定义以及三角形内角和定理即可得出结果.
解答 解:∵△ABC、△DEF和△GMN都是等边三角形,
∴∠GMN=∠MGN=∠DEF=60°,
∵∠1+∠GMN+∠GME=180°,∠2+∠MGN+∠EGM=180°,∠3+∠DEF+∠MEG=180°,
∴∠1+∠GMN+∠GME+∠2+∠MGN+∠EGM+∠3+∠DEF+∠MEG=3×180°,
∵∠GME+∠EGM+∠MEG=180°,
∴∠1+∠2+∠3=3×180°-180°-3×60°=180°;
故选:D.
点评 本题考查了等边三角形的性质、三角形内角和定理、平角的定义;熟练掌握等边三角形的性质和三角形内角和定理是解决问题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{5}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
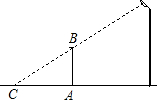 如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.
如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com