
【题目】如图,∠MON=120°,△ABC是等边三角形,O点是边BC的中点,将△ABC绕点O逆时针旋转一定的角度,OM与边AB相交于点D,ON与边AC(或AC的延长线)相交于点E.
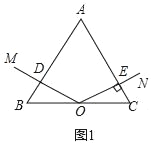
(1)如图1,若OD⊥AB,垂足为D,BC=4,求CE的长;
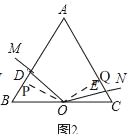
(2)如图2,当ON与AC边交于点E时,求证:BD+CE=![]() BC;
BC;
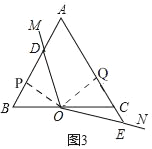
(3)如图3,当ON与AC边的延长线交于点E时,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BD、BC、CE之间的数量关系.

【答案】(1)1(2)见解析(3)不成立
【解析】【试题分析】(1)如图1,△ABC是等边三角形,根据等边三角形的性质得:∠B=∠C=60°,
因为点O是线段BC的中点,
根据中点的定义得:BO=OC=![]() BC=2.
BC=2.
因为OD⊥AB,得∠ODB=∠ODA=90°,
根据三角形内角和定理得:∠BOD=180°﹣60°﹣90°=30°,
在Rt△OBD中,BD=![]() OB=
OB=![]() ×2=1;
×2=1;
又∠OEA=360°﹣60°﹣90°﹣120°=90°,
即∠OEC=90°,
根据AAS得:△OBD≌△OCE,
根据全等三角形的性质得:CE=BD=1;
(2)转化为(1),利用相同的思路证明即可;
(3)(2)中的结论不成立,线段BD、BC、CE之间的数量关系为BD﹣CE=![]() BC.
BC.
理由: 由(1)知△OBP≌△OCQ,
根据全等三角形的性质得:BP=CQ,OP=OQ.
因为∠A=60°,利用四边形的内角和得:∠POQ=360°﹣60°﹣90°﹣90°=120°.
因为∠DOE=120°,利用等式的 性质得:∠POD=∠QOE.
根据ASA得:△POD≌△QOE,根据全等三角形的性质得:PD=EQ.在Rt△BOP中,∠B=60°,根据30°所对的直角边是斜边的一半得:BP=![]() OB=
OB=![]() BC
BC
得证:BD﹣CE=BP+PD﹣CE=CQ+EQ﹣CE=CQ+CQ+CE﹣CE=2CQ=2BP=2×![]() BC=
BC=![]() BC.
BC.
【试题解析】
(1)如图1,∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵点O是线段BC的中点,
∴BO=OC=![]() BC=2.
BC=2.
∵OD⊥AB,得∠ODB=∠ODA=90°,
∴∠BOD=180°﹣60°﹣90°=30°,
在Rt△OBD中,BD=![]() OB=
OB=![]() ×2=1;
×2=1;
又∠OEA=360°﹣60°﹣90°﹣120°=90°,
∴∠OEC=90°,
∴△OBD≌△OCE,
∴CE=BD=1;

(2)过点O作OP⊥AB于P,作OQ⊥AC于Q,如图2,
则有∠OPD=∠OQE=90°.
同(1)的方法得,△OBP≌△OCQ,
∴OP=OQ.
∵∠A=60°,
∴∠POQ=360°﹣60°﹣90°﹣90°=120°.
∵∠DOE=120°,
∴∠POD=∠QOE.
∴△POD≌△QOE,
∴PD=EQ.
∴BD+CE=BP+PD+CE=BP+EQ+CE=BP+CQ=2BP=2×![]() OB=
OB=![]() BC.
BC.

(3)(2)中的结论不成立,线段BD、BC、CE之间的数量关系为BD﹣CE=![]() BC.
BC.
理由:如图3,过点O作OP⊥AB于P,作OQ⊥AC于Q,
则有∠OPD=∠OQE=90°.
由(1)知△OBP≌△OCQ,
∴BP=CQ,OP=OQ.
∵∠A=60°,
∴∠POQ=360°﹣60°﹣90°﹣90°=120°.
∵∠DOE=120°,
∴∠POD=∠QOE.
∴△POD≌△QOE,
∴PD=EQ.
在Rt△BOP中,∠B=60°,
∴BP=![]() OB=
OB=![]() BC
BC
∴BD﹣CE=BP+PD﹣CE=CQ+EQ﹣CE=CQ+CQ+CE﹣CE=2CQ=2BP=2×![]() BC=
BC=![]() BC.
BC.



科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
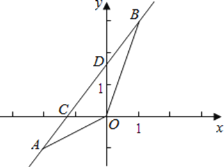
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
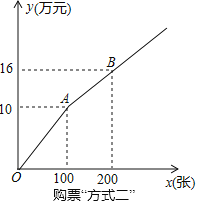
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
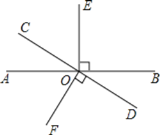
(1)图中与∠AOF互余的角是 _________ ;与∠COE互补的角是 _______ __ .(把符合条件的角都写出来)
(2)如果∠AOC=![]() ∠EOF,求∠AOC的度数.
∠EOF,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,按如下步骤作图:①以点A为圆心,AB长为半径画弧;②以点C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
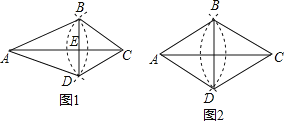
(1)填空:△ABC≌△ ;AC和BD的位置关系是
(2)如图2,当AB=BC时,猜想四边形ABCD是什么四边形,并证明你的结论.
(3)在(2)的条件下,若AC=8cm,BD=6cm,则点B到AD的距离是 cm,若将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划每天生产零件![]() 个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)由表可知该厂星期四生产零件 个,这周实际生产零件 个.(用含![]() 的代数式表示)
的代数式表示)
(2) 产量最高日比最低日多生产零件 个.
(3) 若该周厂计划每天生产零件数是![]() ,每个零件应支付工资
,每个零件应支付工资![]() 元,且每天超计划数的零件每个另奖
元,且每天超计划数的零件每个另奖![]() 元,那这周实际应支付工资多少元?
元,那这周实际应支付工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宿豫区实验初中的图书室平均每天借出图书50册.如果某天借出53册,就记作+3;如果某天借出40册,就记作-10.上星期我校图书室借出图书记录如下:

(1)上星期五借出图书多少册?
(2)上星期二比上星期五多借出图书多少册?
(3)上星期总共借出图书多少册?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com