练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．如图，在?ABCD中，若点E、F分别是AB，CD的中点，连接AF，CE，DE，BF．DE与AF相交于点G，CE与BF相交于点H．求证：四边形GEHF是平行四边形．

    分析 由平行四边形的性质和已知条件得出四边形AECF是平行四边形，得出AF∥CE．同理：DE∥BF，由平行四边形的判定方法即可得出结论．

    解答 证明：∵四边形ABCD是平行四边形，
    ∴AB∥CD，AB=CD，
    ∵E是AB中点，F是CD中点，
    ∴AE=CF，AE∥CF，
    ∴四边形AECF是平行四边形，
    ∴AF∥CE．
    同理：DE∥BF，
    ∴四边形GEHF是平行四边形．

    点评 考查了平行四边形的判定与性质；熟练掌握平行四边形的判定与性质，通过证明平行四边形得出AF∥CE．DE∥BF是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）8+（-10）+（-2）-（-5）；
    （2）$-\frac{1}{3}×{（{-3}）^2}$；
    （3）$（{-12}）×（{-\frac{1}{2}-\frac{2}{3}+\frac{3}{4}}）$；
    （4）$-{2^2}-5×\frac{1}{5}+|{-3}|$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．画出y=$\frac{1}{2}$x2-6x+3的图象（草图），并写出其顶点坐标、对称轴和最值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．已知抛物线的顶点坐标是P（1，3），且开口向下，下列说法正确的是（　　）
    A．当x≤1时，y随x的增大而减小B．当x≥1时，y随x的增大而增大
    C．当x＜3时，y随x的增大而减小D．当x＞3时，y随x的增大而减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

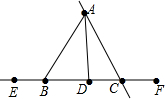    4．如图所示，图中能够写出的射线有9条，它们分别是射线AC，CA，EB，BE，BD，DB，DC，CD，FC；线段有13条，它们分别是线段AB，AD，AC，EB，ED，EC，EF，BC，BC，BF，DC，DF，CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如果3x2yn与-$\frac{1}{2}$xmy是同类项，那么m+2n=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．阅读下列材料，然后回答问题．在进行二次根式的化简运算时，我们有时会碰上形如$\frac{2}{\sqrt{3}+1}$的式子，其实我们还可以将其进一步简化：$\frac{2}{\sqrt{3}+1}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}）^{2}-{1}^{2}}$=$\sqrt{3}$-1．以上这种化简的步骤叫做分母有理化．
    请用上面的方法化简：$\frac{1}{2-\sqrt{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

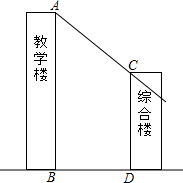    18．如图所示，综合楼高12m，两楼相距5m，在下午某一时刻太阳光与水平面的夹角为30°，当教学楼影子顶端A刚好落在综合楼顶端C处时，问教学楼的高度约为多少米？（$\sqrt{3}$≈1.732，结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．求一次函数y=$\frac{1}{2}$x-1的图象与一次函数y=-x-3的图象的交点坐标，并求出这两个函数的图象与x轴所围成的三角形的面积．

    查看答案和解析>>

    同步练习册答案