
【题目】已知![]() 三点在数轴上所对应的数分别为
三点在数轴上所对应的数分别为![]() 且
且![]() 满足
满足![]() .动点
.动点![]() 从点
从点![]() 出发,以2单位/秒的速度向右运动,同时,动点
出发,以2单位/秒的速度向右运动,同时,动点![]() 从点
从点![]() 出发,以1单位秒的速度向左运动,线段
出发,以1单位秒的速度向左运动,线段![]() 为“变速区”,规则为: 从点
为“变速区”,规则为: 从点![]() 运动到点
运动到点![]() 期间速度变为原来的一半,之后立刻恢复原速,从点
期间速度变为原来的一半,之后立刻恢复原速,从点![]() 运动到点
运动到点![]() 期间速度变为原来的两倍,之后也立刻恢复原速.当点
期间速度变为原来的两倍,之后也立刻恢复原速.当点![]() 到达点
到达点![]() 时,两点都停止运动.设运动的时间为
时,两点都停止运动.设运动的时间为![]() 秒.
秒.
(1) ![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)①动点![]() 从点
从点![]() 运动至点
运动至点![]() 时,求
时,求![]() 的值;
的值;
②![]() 两点相遇时,求相遇点在数轴上所对应的数;
两点相遇时,求相遇点在数轴上所对应的数;
(3)若点![]() 为线段
为线段![]() 中点,当
中点,当![]() ________秒时,
________秒时,![]() .
.
![]()
【答案】(1)![]() ;(2)①19s;②
;(2)①19s;②![]() ;(3)当
;(3)当![]() 秒时,
秒时,![]() .
.
【解析】
(1)根据平方和绝对值的非负性计算即可求出a和b的值,再根据两点间的距离公式即可求出AC的长度;
(2)①分别求出AO,BO和BC的距离,再根据“时间=路程÷速度”计算即可得出答案;②设P点在数轴上所对应的数为y,根据题意列出方程![]() ,解方程即可得出答案;
,解方程即可得出答案;
(3)根据线段中点的性质求出点D的坐标,设时间为t,分五种情况进行讨论,分别求出每种情况下点M和点N的坐标,再根据两点间的距离公式求出MD和ND,令MD=ND,解方程即可得出答案.
解:(1)![]() ;
;
(2)①∵![]()
∴![]()
∴动点![]() 从点
从点![]() 运动至点
运动至点![]() 时,
时,![]() ;
;
②设![]() 两点在
两点在![]() 点相遇,
点相遇,![]() 点在数轴上所对应的数为
点在数轴上所对应的数为![]() .
.
易知点![]() 落在线段
落在线段![]() 段,依题意有:
段,依题意有: ![]()
解得: ![]()
∴![]() 两点相遇时,求相遇点
两点相遇时,求相遇点![]() 在数轴上所对应的数为
在数轴上所对应的数为![]() .
.
(3)若点![]() 为线段
为线段![]() 中点,则D在数轴上表示的数为5
中点,则D在数轴上表示的数为5
设时间为t时,MD=ND
①当点N在CB上,点M在AO上运动时,M=-10+2t,N=18-t
则MD=15-2t,ND=13-t
即15-2t=13-t,解得t=2;
②当点N在CB上,点M在OD上运动时,M=t-5,N=18-t
则MD=10-t,ND=13-t
即10-t=13-t,无解;
③当点N在OB上,点M在OD上运动时,M=t-5,N=10-2(t-8)
则MD=10-t,ND=5-2(t-8)
即10-t=5-2(t-8),解得t=11;
④当点N在OB上,点M在DB上运动时,M=t-5,N=26-2t
则MD=t-10,ND=21-2t
即t-10=21-2t,解得t=![]() ;
;
⑤当点N在OA上,点M在BC上运动时,M=2t-20,N=13-t
则MD=2t-25,ND=t-8
即2t-25=t-8,解得t=17;
综上所述,当![]() 秒时,
秒时,![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中点![]() ,
,![]() ,以
,以![]() 为顶点在第一象限内作正方形
为顶点在第一象限内作正方形![]() .反比例函数
.反比例函数![]() 、
、![]() 分别经过
分别经过![]() 、
、![]() 两点(1)如图2,过
两点(1)如图2,过![]() 、
、![]() 两点分别作
两点分别作![]() 、
、![]() 轴的平行线得矩形
轴的平行线得矩形![]() ,现将点
,现将点![]() 沿
沿![]() 的图象向右运动,矩形
的图象向右运动,矩形![]() 随之平移;
随之平移;
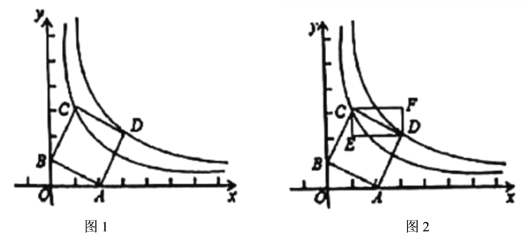
①试求当点![]() 落在
落在![]() 的图象上时点
的图象上时点![]() 的坐标_____________.
的坐标_____________.
②设平移后点![]() 的横坐标为
的横坐标为![]() ,矩形的边
,矩形的边![]() 与
与![]() ,
,![]() 的图象均无公共点,请直接写出
的图象均无公共点,请直接写出![]() 的取值范围____________.
的取值范围____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2个C型模具和1个D型模具;用1块B型钢板可制成1个C型模具和3个D型模具,现准备A、B型钢板共100块,并全部加工成C、D型模具.
(1)若B型钢板的数量是A型钢板的数量的两倍还多10块,求A、B型钢板各有多少块?
(2)若销售C、D型模具的利润分别为80元/块、100元/块,且全部售出.
①当A型钢板数量为25块时,那么共可制成C型模具 个,D型模具 个;
②当C、D型模具全部售出所得的利润为34400元,求A型钢板有多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是18,点E是AB边上的一个动点,点F是CD边上一点,![]() ,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点
,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在直线BC上时,线段AE的长为________.
落在直线BC上时,线段AE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
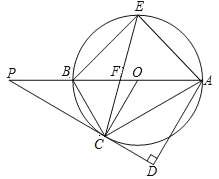
【题目】如图所示,AB 是⊙O 的直径,P 为 AB 延长线上的一点,PC 切⊙O 于点 C,AD⊥PC, 垂足为 D,弦 CE 平分∠ACB,交 AB 于点 F,连接 AE.
(1)求证:PC=PF;
(2)若 tan∠ABC=![]() ,AE=5
,AE=5![]() ,求线段 PC 的长.
,求线段 PC 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科普小组有5名成员,身高(单位:cm)分别为:160,165,170,163,172,把身高160 cm的成员替换成一位165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数变小,方差变小B.平均数变大,方差变大
C.平均数变大,方差不变D.平均数变大,方差变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、CD、EF相交于O点,AB⊥CD,

(1)写出∠AOF, ∠DOE的邻补角;
(2)写出∠AOE, ∠DOF的对顶角;
(3)如果∠DOF=38°求∠AOF和∠AOE的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
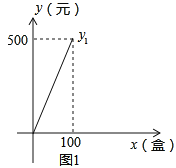
方案一:从包装盒加工厂直接购买所需的费![]() 与包装盒数
与包装盒数![]() 满足如图1所示的函数关系.
满足如图1所示的函数关系.
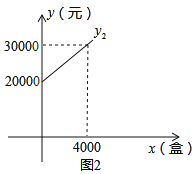
方案二:租赁机器自己加工,所需费用![]() (包括租赁机器的费用和生产包装盒的费用)与包装盒数
(包括租赁机器的费用和生产包装盒的费用)与包装盒数![]() 满足如图2所示的函数关系.根据图回答下列问题:
满足如图2所示的函数关系.根据图回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1、y2与x的函数关系式,如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com