
 按如下方法,将△ABC的三边缩小的原来的$\frac{1}{2}$,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的是( )
按如下方法,将△ABC的三边缩小的原来的$\frac{1}{2}$,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的是( )| A. | △ABC与△DEF不是位似图形 | B. | $\frac{OE}{OB}$=$\frac{1}{3}$ | ||
| C. | △ABC与△DEF的周长比为1:2 | D. | △ABC与△DEF的面积比为4:1 |
分析 根据位似的定义对A进行判断;根据相似三角形的性质对B、C、D进行判断.
解答 解:A、△ABC与△DEF是位似图形,所以A选项的说法错误;
B、因为AO、BO、CO的中点分别为D、E、F,则OE:OB=EF:BC=1:2,所以B选项的说法错误;
C、因为△ABC与△DEF的相似比为2,所以△ABC与△DEF的周长比为2,所以C选项的说法错误;
D、因为△ABC与△DEF的相似比为2,所以△ABC与△DEF的面积比为4:1,所以D选项的说法正确.
故选D.
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.也考查了相似的性质.


科目:初中数学 来源: 题型:填空题
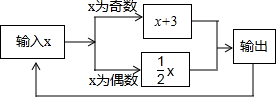 有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2017次输出的结果是1.
有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2017次输出的结果是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com