
����Ŀ����2017��������21�⣬9�֣���֪����![]() ��ͼ����x�������������㣮
��ͼ����x�������������㣮
��1����m��ȡֵ��Χ����д����mȡ��Χ���������ʱ�����Ľ���ʽ��
��2���⣨1������õĺ�����ΪC1��
�ٵ�n��x�ܩ�1ʱ��y��ȡֵ��Χ��1��y�ܩ�3n����n��ֵ��
�ں���![]() ��ͼ���ɺ���C1��ͼ��ƽ�Ƶõ����䶥��P������ԭ��ΪԲ�ģ��뾶Ϊ
��ͼ���ɺ���C1��ͼ��ƽ�Ƶõ����䶥��P������ԭ��ΪԲ�ģ��뾶Ϊ![]() ��Բ�ڻ�Բ�ϣ��躯��C1��ͼ��ΪM�����P���M�������ʱ����C2�Ľ���ʽ��
��Բ�ڻ�Բ�ϣ��躯��C1��ͼ��ΪM�����P���M�������ʱ����C2�Ľ���ʽ��
���𰸡���1��m��![]() ��m��0��
��m��0��![]() ����2���٩�2����
����2���٩�2����![]() ��
��
�������������������1������ͼ����x�������������㣬��ú���Ϊ���κ����ҡ���0���ʴ˿ɵõ�����m�IJ���ʽ�飬�Ӷ������m��ȡֵ��Χ��
��2������������ߵĶԳ��ᣬ��n��x�ܩ�1ʱ������ͼ��λ�ڶԳ������࣬y��x���������С������x=nʱ��y�����ֵ��3n��Ȼ��x=n��y=��3n������⼴�ɣ�
��3������õ�M�����꣬Ȼ������õ�MP����Բ��ʱ��PM�����ֵ���ʴ˿���õ�P�����꣬�Ӷ��ɵõ�����C2�Ľ���ʽ��
�����������1��������ͼ����x�����������㣬��m��0��[����2m��5��]2��4m��m��2����0����ã�m��![]() ��m��0��
��m��0��
��mΪ���������������������m=2���������Ľ���ʽΪ![]() ��
��
��2�������ߵĶԳ���Ϊx=![]() =
=![]() ��
��
��n��x�ܩ�1��![]() ��a=2��0������n��x�ܩ�1ʱ��y��x���������С������x=nʱ��y=��3n����2n2+n=��3n�����n=��2��n=0����ȥ������n��ֵΪ��2��
��a=2��0������n��x�ܩ�1ʱ��y��x���������С������x=nʱ��y=��3n����2n2+n=��3n�����n=��2��n=0����ȥ������n��ֵΪ��2��
��3����![]() =
=![]() ����M��
����M��![]() ��
��![]() ����
����
��ͼ��ʾ��

����P��OM����O�Ľ��㴦ʱ��PM�����ֵ��
��ֱ��OM�Ľ���ʽΪy=kx������M���������ã�![]() ����ã�k=
����ã�k=![]() ����OM�Ľ���ʽΪy=
����OM�Ľ���ʽΪy=![]() x��
x��
���P��������x��![]() x����
x����
�������ľ��빫ʽ��֪��OP=![]() =5����ã�x=2��x=��2����ȥ��������P������Ϊ��2��1����������P���M�������ʱ����C2�Ľ���ʽΪ
=5����ã�x=2��x=��2����ȥ��������P������Ϊ��2��1����������P���M�������ʱ����C2�Ľ���ʽΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧΪ�˽⺢���Ƕԡ������й��� ����ǿ���ԡ� ����ս�����ܡ� ��������˵�ҡ� ���й�ʫ�ʴ�ᡷ���ֵ��ӽ�Ŀ��ϲ���̶ȣ�������ߡ��ˡ����꼶��ȡ�˲���ѧ�����е��飨ÿ��ֻ��ѡ��һ��ϲ���ĵ��ӽ�Ŀ����������õ����ݽ������������Ƴ�����������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺

��1�����ε��鹲��ȡ��_________________��ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�ϲ���������й�����Ŀ���������ڵ����ε�Բ�Ľ���__________�ȡ�
��4������У��1500��ѧ���������ϲ������ǿ���ԡ���Ŀ��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
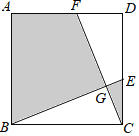
����Ŀ����ͼ����������ABCD�У�AB=3����E��F�ֱ���CD��AD�ϣ�CE=DF��BE��CF�ཻ�ڵ�G����ͼ����Ӱ���ֵ������������ABCD�����֮��Ϊ2��3������BCG���ܳ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() ���ʾ������-8��
���ʾ������-8��![]() ���ʾ������2.���߶�
���ʾ������2.���߶�![]() ����
����![]() �ڵ�
�ڵ�![]() ���Ҳࣩ���ӵ�
���Ҳࣩ���ӵ�![]() ���
���![]() �غϵ�λ�ó�������ÿ��2����λ���ٶ������˶����˶�ʱ��Ϊ
�غϵ�λ�ó�������ÿ��2����λ���ٶ������˶����˶�ʱ��Ϊ![]() ��.
��.
![]()
��1������֪��![]() ��ʾ������-6�������
��ʾ������-6�������![]() ��ʾ������
��ʾ������
���ú���![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() ��ʾ������
��ʾ������
��2����![]() ʱ����
ʱ����![]() ��ֵ.
��ֵ.
��3�����ʵ��߶�![]() ��ʲôλ��ʱ��
��ʲôλ��ʱ��![]() ��
��![]() ��ֵʼ�ձ��ֲ��䣿���������ֵ��˵����ʱ�߶�
��ֵʼ�ձ��ֲ��䣿���������ֵ��˵����ʱ�߶�![]() ��λ��.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ4����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F�㣮����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬����CDM�ܳ�����СֵΪ8�����ABC�����Ϊ��������
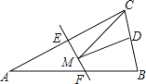
A.12B.16C.24D.32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ160Ԫ��120Ԫ��A��B�����ͺŵĵ���ȣ�����ǽ����ܵ���������������ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 4̨ | 1200Ԫ |
�ڶ��� | 5̨ | 6̨ | 1900Ԫ |
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����������ò�����7500Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�50̨����A���ͺŵĵ��������ܲɹ�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA=2���Ե�AΪԲ�ģ�1Ϊ�뾶����A��OA���ӳ��߽��ڵ�C������A��OA�Ĵ��ߣ��������A��һ������ΪB������BC
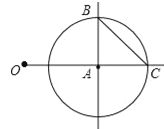
��1���߶�BC�ij����� ��
��2������ͼ�а�����Ҫ����һ���������ش����⣺
���Ե� ΪԲ�ģ����߶� �ij�Ϊ�뾶������������BA���ڵ�D��ʹ�߶�OD�ij�����![]() ��
��
����OD����OD�ϻ�����P��ʹOP�ó�����![]() ����д����������˵�����ɣ�
����д����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��F��BD�ϣ���BF��DE��
��1��д��ͼ����������Ϊȫ�ȵ������Σ�
��2���ӳ�AE��BC���ӳ�����G���ӳ�CF��DA���ӳ�����H���벹ȫͼ�Σ���֤���ı���AGCH��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���ACB��90����CD��AB�ڵ�D����A��30��������˵��������ǣ�������
A. AC��2CDB. AD��2CDC. AD��3BDD. AB��2BC
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com