
����Ŀ����ͼ,�ڡ�ABC��.AC=BC=5.AB=6.CD��AB������.��P�ӵ�C��������ÿ��2.5����λ���ȵ��ٶ���C-D-C�˶�.�ڵ�P������ͬʱ����QҲ�ӵ�C��������ÿ��2����λ���ȵ��ٶ��ر�CA���A�˶�.��һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�����P�˶���ʱ��Ϊt��.
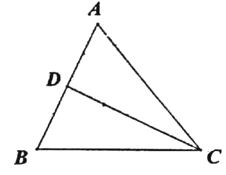
��1���ú�t�Ĵ���ʽ��ʾCP��CQ�ij���.
��2���ú�t�Ĵ���ʽ��ʾ��CPQ�����.
��3������CPQ���CAD����ʱ��ֱ��д��t��ȡֵ��Χ.
���𰸡���1����0��t��![]() ʱ��CP=2.5t��CQ=2t����
ʱ��CP=2.5t��CQ=2t����![]() ʱ��CP=8-2.5t��CQ=2t��
ʱ��CP=8-2.5t��CQ=2t��
��2����0��t��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ��2.5t��
��2.5t��![]() ��2t=
��2t=![]() ����
����![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ����8-2.5t����
����8-2.5t����![]() ��2t=
��2t=![]() .
.
��3��0��t��![]() ��
��![]() s
s
��������
��1�����������Σ���0��t��![]() ʱ����
ʱ����![]() ��t
��t![]() ʱ���ֱ���⼴�ɣ�
ʱ���ֱ���⼴�ɣ�
��2�����������Σ���0��t��![]() ʱ����
ʱ����![]() ��t��
��t��![]() ʱ������S��CPQ=
ʱ������S��CPQ=![]() PCsin��ACDCQ�ֱ���⼴�ɣ�
PCsin��ACDCQ�ֱ���⼴�ɣ�
��3�����������Σ���0��t��![]() ������֤����QCP�ס�DCA����
������֤����QCP�ס�DCA����![]() ��t
��t![]() ����QPC=90��ʱ����QPC�ס�ADC������������⼴�ɣ�
����QPC=90��ʱ����QPC�ס�ADC������������⼴�ɣ�
�⣺��1����CA=CB��AD=BD=3��
��CD��AB��
���ADC=90����
��CD=![]() =
=![]() =4��
=4��
��0��t��![]() ʱ��CP=2.5t��CQ=2t��
ʱ��CP=2.5t��CQ=2t��
��![]() ʱ��CP=8-2.5t��CQ=2t��
ʱ��CP=8-2.5t��CQ=2t��
��2����sin��ACD=![]() =
=![]() ��
��
�൱0��t��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ��2.5t��
��2.5t��![]() ��2t=
��2t=![]()
��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ����8-2.5t����
����8-2.5t����![]() ��2t=
��2t=![]() .
.
��3���ٵ�0��t��![]() ʱ��
ʱ��
��CP=2.5t��CQ=2t��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��![]() ��
��
�ߡ�PCQ=��ACD��
���QCP�ס�DCA��
��0��t��![]() ʱ����QCP�ס�DCA��
ʱ����QCP�ס�DCA��
�ڵ�![]() ʱ������
ʱ������
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��������������������t��ֵΪ��0��t��![]() ��
��![]() sʱ����QCP�ס�DCA��
sʱ����QCP�ס�DCA��


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ֱ������![]() ����ƽ��ֱ������ϵ�У���֪
����ƽ��ֱ������ϵ�У���֪![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ��
��

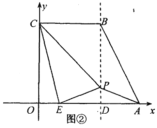
��1����֤��![]() ��
��
��2����ͼ�ڣ�����![]() ��
��![]() ����
����![]() ����
����![]() ��ֱ��
��ֱ��![]() ���˶�������
���˶�������![]() ��
��![]() ��
��
�ٵ�![]() ���ܳ����ʱ�����
���ܳ����ʱ�����![]() �����ꣻ
�����ꣻ
�������![]() ��
��![]() ���Ϸ���������
���Ϸ���������![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ʡ�����������ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 10 | 8 | 9 | 8 | 10 | 9 |
�� | 10 | 7 | 10 | 10 | 9 | 8 |
��1�����ݱ����е����ݣ��ֱ����ס��ҵ�ƽ���ɼ���
��2���ֱ����ס������β��Գɼ��ķ��
��3�����ݣ�1������2������Ľ��������Ϊ�Ƽ�˭�μ�ʡ���������ʣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m������,����x�ķ���mx2-��m-1��x+1=0�����������̵ĸ�Ϊ�� ����
A. ![]() B. x=-1 C. x1=1,
B. x=-1 C. x1=1,![]() D. ����������
D. ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ҵ������̵�1-6�����ۼס�������Ʒ�Ʊ����������ͼ��ʾ����λ��̨����
��1���ֱ�����̵����ʱ���ڼס�������Ʒ�Ʊ�������������ƽ�����ͷ��
��2�����ݼ�����������ͳ��ͼ���Ը��̵���ɹ�������Ʒ�Ʊ��������������飬��˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��BDƽ����ABC��AC�ڵ�D��AE��BD��CB���ӳ����ڵ�E������E=35��������BAC�Ķ���Ϊ�� ��

A. 40�� B. 45�� C. 60�� D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A��B���㣬��y�ύ�ڵ�C���Գ���Ϊֱ��x=��1����B������Ϊ��1��0���������н��ۣ���AB=4����b2��4ac��0����ab��0����a2��ab+ac��0��������ȷ�Ľ����У�����������
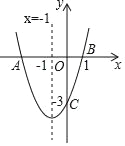
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��G��������ABCD�Խ���AC��һ�㣬��GE��AD��GF��AB������ֱ�Ϊ��E��F.
��֤���ı���AFGE���ı���ABCD���ƣ�
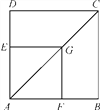
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������C1��y��![]() x2��2x��
x2��2x��![]() ����x���ཻ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����֪M��4��0������P���������ϵĵ㣬�������Ϊ6����DΪ�����ߵĶ��㣮
����x���ཻ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����֪M��4��0������P���������ϵĵ㣬�������Ϊ6����DΪ�����ߵĶ��㣮
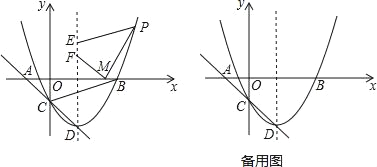
��1����S��ABC��
��2����E��F�������߶Գ����ϵ������㣬����֪E��2��a+![]() ����F��2��a������aΪ��ֵʱ���ı���PEFM�ܳ���С����˵�����ɣ�
����F��2��a������aΪ��ֵʱ���ı���PEFM�ܳ���С����˵�����ɣ�
��3����������C1�Ƶ�D��ת180���õ�������C2��ֱ��CDƽ�ƣ�ƽ�ƺ�������߽�y���ڵ�Q������ΪR��ƽ�ƺ��Ƿ���������������ߣ�ʹ��CRQΪ���������Σ������ڣ��������ʱ�����ߵĽ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com