
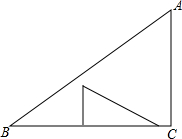
 在△ABC中,∠C=90°,AC=3,BC=4,两直角边分别为1,2的三角形纸片按如图所示放置,若该纸片在△ABC内任意平移,求△ABC内不能被平移到的部分的面积和.
在△ABC中,∠C=90°,AC=3,BC=4,两直角边分别为1,2的三角形纸片按如图所示放置,若该纸片在△ABC内任意平移,求△ABC内不能被平移到的部分的面积和. 分析 当CD边平移到C′D′位置时,过D′F⊥AC于F,根据全等三角形的想知道的D′F=CE=2,C′F=DE=1,根据相似三角形的性质得到$\frac{D′F}{BC}=\frac{AF}{AC}$,于是得到S△AD′C′=$\frac{1}{2}$AC′•D′F=$\frac{1}{2}×$$\frac{5}{2}$×2=$\frac{5}{2}$,当ED边平移到E′D″位置时,根据相似三角形的性质得到$\frac{D″E′}{AC}=\frac{BE′}{BC}$,于是得到S△BD″E′=$\frac{1}{2}$BE′•D″E′=$\frac{1}{2}$×$\frac{4}{3}$×1=$\frac{2}{3}$,即可得到结论.
解答 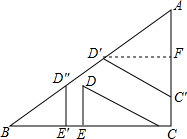 解:当CD边平移到C′D′位置时,
解:当CD边平移到C′D′位置时,
过D′F⊥AC于F,
则△C′D′F≌△CDE,
∴D′F=CE=2,C′F=DE=1,
∵∠C=90°,
∴∠AFD′=∠C,
∴D′F∥BC,
∴△AD′F≌△ABC,
∴$\frac{D′F}{BC}=\frac{AF}{AC}$,
∴AF=$\frac{3}{2}$,
∴S△AD′C′=$\frac{1}{2}$AC′•D′F=$\frac{1}{2}×$$\frac{5}{2}$×2=$\frac{5}{2}$,
当ED边平移到E′D″位置时,
∴D″E′=1,
∵D″E′∥AC,
∴△BD″E′∽△ABC,
∴$\frac{D″E′}{AC}=\frac{BE′}{BC}$,
∴BE′=$\frac{4}{3}$,
∴S△BD″E′=$\frac{1}{2}$BE′•D″E′=$\frac{1}{2}$×$\frac{4}{3}$×1=$\frac{2}{3}$,
∴△ABC内不能被平移到的部分的面积和=S△AD′C+S△BD″E′=$\frac{19}{6}$.
点评 本题考查了平移的性质,三角形面积的计算,相似三角形的判定和性质,正确的理解题意,知道△ABC内不能被平移到的部分的面积和=S△AD′C+S△BD″E′是解题的关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
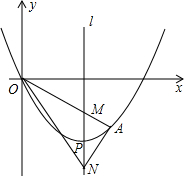 如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.
如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com