
【题目】红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的 日销售量(件)与时间(天)的关系如下表:
时间(天) | 1 | 3 | 6 | 10 | 36 | … |
日销售量(件) | 94 | 90 | 84 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与t时间(天)的函数关系式为:y1=![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—
t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—![]() t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
(1)认真分析上表中的数量关系,利用学过的一次函数、二次函数 、反比例函数的知识确定一个满足这些数据之间的函数关系式;
(2)请预测未来40天中那一天的销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
【答案】(1)y=﹣2t+96;(2)当t=14时,利润最大,最大利润是578元;(3)3≤a<4.
【解析】
(1)通过观察表格中的数据日销售量与时间t是均匀减少的,所以确定m与t是一次函数关系,利用待定系数法即可求出函数关系式;
(2)根据日销售量、每天的价格及时间t可以列出销售利润W关于t的二次函数,然后利用二次函数的性质即可求出哪一天的日销售利润最大,最大日销售利润是多少;
(3)列式表示前20天中每天扣除捐赠后的日销售利润,根据函数的性质求出a的取值范围 .
(1)设数m=kt+b,有![]() ,解得
,解得![]()
∴m=-2t+96,经检验,其他点的坐标均适合以上
析式故所求函数的解析式为m=-2t+96.
(2)设日销售利润为P,
由P=(-2t+96)![]() =t2-88t+1920=(t-44)2-16,
=t2-88t+1920=(t-44)2-16,
∵21≤t≤40且对称轴为t=44,
∴函数P在21≤t≤40上随t的增大而减小,
∴当t=21时,P有最大值为(21-44)2-16=529-16=513(元),
答:来40天中后20天,第2天的日销售利润最大,最大日销售利润是513元.
(3)P1=(-2t+96)![]()
=-![]() +(14+2a)t+480-96n,
+(14+2a)t+480-96n,
∴对称轴为t=14+2a,
∵1≤t≤20,
∴14+2a≥20得a≥3时,P1随t的增大而增大,
又∵a<4,
∴3≤a<4.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
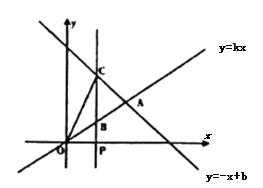
【题目】如图,已知在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点
的图象相交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
(1)求这两个函数解析式.
(2)求![]() 的面积.
的面积.
(3)在坐标轴上存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,请直接写出
为腰的等腰三角形,请直接写出![]() 点的坐标。
点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
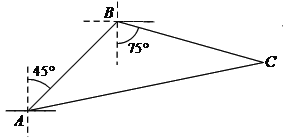
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有a个除颜色外完全相同的红球和白球,其中红球有b个,将盒中的球摇匀后从中任意摸出1个球,记录颜色后将球放回盒中,重复进行这过程,如表记录了某班一次摸球实验情况:
摸球总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
摸到红球数m | 325 | 1336 | 3203 | 6335 | 8073 | 12628 |
摸到红球的频率(精确到0.001) | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
(1)由此估计任意摸出1个球为红球的概率约是 (精确到0.1)
(2)实验结束后,小明发现了一个一般性的结论:盒子中共有a个球,其中红球有b个,则摇匀后从中任意摸出1个球为红球的概率P可以表示为![]() ,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6a,BC=6b,∠D=60°,点E、F、G、H分别在ABCD各边上,且BE=DG=![]() AE,CF=AH=
AE,CF=AH=![]() BF.
BF.
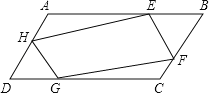
(1)求证:四边形EFGH是平行四边形;
(2)若四边形EFGH是菱形,求![]() 的值;
的值;
(3)四边形EFGH能为正方形吗?若能,请直接写出a、b的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:

(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
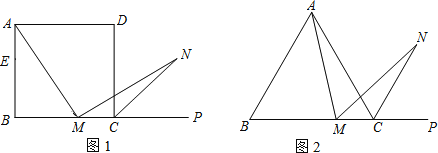
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“一起阅读,共同成长”课外读书周活动,活动后期随机调查了八年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
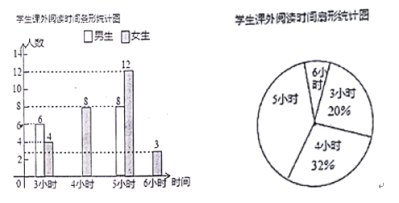
(1)本次调查的学生总数为______人,在扇形统计图中,课外阅读时间为5小时的扇形圆心角度数是______;
(2)请你补全条形统计图;
(3)若全校八年级共有学生![]() 人,估计八年级一周课外阅读时间至少为
人,估计八年级一周课外阅读时间至少为![]() 小时的学生有多少人?
小时的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com