
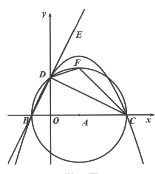
【题目】如图,已知点B的坐标是(-2,0),点C的坐标是(8,0),以线段BC为直径作⊙A,交y轴的正半轴于点D,过B、C、D三点作抛物线.
(1)求抛物线的解析式;
(2)连结BD,CD,点E是BD延长线上一点,∠CDE的角平分线DF交⊙A于点F,连结CF,在直线BE上找一点P,使得△PFC的周长最小,并求出此时点P的坐标;
(3)在(2)的条件下,抛物线上是否存在点G,使得∠GFC=∠DCF,若存在,请直接写出点G的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)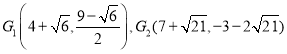
【解析】
(1)由BC是直径证得∠OCD=∠BDO,从而得到△BOD∽△DOC,根据线段成比例求出OD的长,
设抛物线解析式为y=a(x+2)(x-8),将点D坐标代入即可得到解析式;
(2)利用角平分线求出![]() ,得到
,得到![]() ,从而得出点F的坐标(3,5),再延长延长CD至点
,从而得出点F的坐标(3,5),再延长延长CD至点![]() ,可使
,可使![]() ,得到
,得到![]() (-8,8),求出
(-8,8),求出![]() F的解析式,与直线BD的交点坐标即为点P,此时△PFC的周长最小;
F的解析式,与直线BD的交点坐标即为点P,此时△PFC的周长最小;
(3)先假设存在,①利用弧等圆周角相等把点D、F绕点A顺时针旋转90![]() ,使点F与点B重合,点G与点Q重合,则Q1(7,3),符合
,使点F与点B重合,点G与点Q重合,则Q1(7,3),符合![]() ,求出直线FQ1的解析式,与抛物线的交点即为点G1,②根据对称性得到点Q2的坐标,再求出直线FQ2的解析式,与抛物线的交点即为点G2,由此证得存在点G.
,求出直线FQ1的解析式,与抛物线的交点即为点G1,②根据对称性得到点Q2的坐标,再求出直线FQ2的解析式,与抛物线的交点即为点G2,由此证得存在点G.
(1)∵以线段BC为直径作⊙A,交y轴的正半轴于点D,
∴∠BDO+∠ODC=90![]() ,
,
∵∠OCD+∠ODC=90![]() ,
,
∴∠OCD=∠BDO,
∵∠DOC=∠DOB=90![]() ,
,
∴△BOD∽△DOC,
∴![]() ,
,
∵B(-2,0),C(8,0),
∴![]() ,
,
解得OD=4(负值舍去),∴D(0,4)
设抛物线解析式为y=a(x+2)(x-8),
∴4=a(0+2)(0-8),
解得a=![]() ,
,
∴二次函数的解析式为y=![]() (x+2)(x-8),即
(x+2)(x-8),即![]() .
.
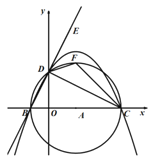
(2)∵BC为⊙A的直径,且B(-2,0),C(8,0),
∴OA=3,A(3,0),
∴点E是BD延长线上一点,∠CDE的角平分线DF交⊙A于点F,
∴![]() ,
,
连接AF,则![]() ,
,
∵OA=3,AF=5
∴F(3,5)
∵∠CDB=90![]() ,
,
∴延长CD至点![]() ,可使
,可使![]() ,
,
∴![]() (-8,8),
(-8,8),
连接![]() F叫BE于点P,再连接PF、PC,
F叫BE于点P,再连接PF、PC,
此时△PFC的周长最短,
解得![]() F的解析式为
F的解析式为![]() ,
,
BD的解析式为y=2x+4,
可得交点P![]() .
.

(3)存在;假设存在点G,使∠GFC=∠DCF,
设射线GF交⊙A于点Q,
①∵A(3,0),F(3,5),C(8,0),D(0,4),
∴把点D、F绕点A顺时针旋转90![]() ,使点F与点B重合,点G与点Q重合,则Q1(7,3),符合
,使点F与点B重合,点G与点Q重合,则Q1(7,3),符合![]() ,
,
∵F(3,5),Q1(7,3),
∴直线FQ1的解析式为![]() ,
,
解 ,得
,得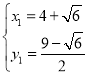 ,
,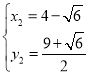 (舍去),
(舍去),
∴G1![]() ;
;
②Q1关于x轴对称点Q2(7,-3),符合![]() ,
,
∵F(3,5),Q2(7,3),
∴直线FQ2的解析式为y=-2x+11,
解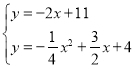 ,得
,得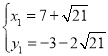 ,
,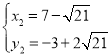 (舍去),
(舍去),
∴G2![]()
综上,存在点G![]() 或
或![]() ,使得∠GFC=∠DCF.
,使得∠GFC=∠DCF.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上一点,点C在直径AB的延长线上,且∠CDB=∠CAD,过点A作⊙O的切线,交CD的延长线于点E.

(1)判定直线CD与⊙O的位置关系,并说明你的理由;
(2)若CB=4,CD=8,①求圆的半径.②求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在正方形ABCD中,点E、F分别为边BC与CD上的点,且∠EAF=45°,AE与AF分别交对角线BD于点M、N,则下列结论正确的是_____.
①∠BAE+∠DAF=45°;②∠AEB=∠AEF=∠ANM;③BM+DN=MN;④BE+DF=EF
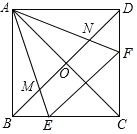
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为( )
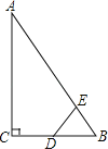
A.4或5B.4或7C.4或5或7D.4或7或9
查看答案和解析>>
科目:初中数学 来源: 题型:
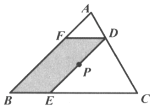
【题目】如图,已知点P是△ABC的重心,过P作AB的平行线DE,分别交AC于点D,交BC于点E,作DF//BC,交AB于点F,若四边形BEDF的面积为4,则△ABC的面积为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
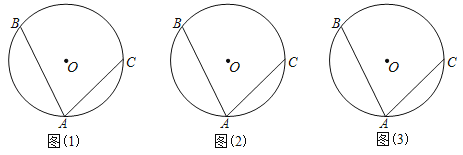
【题目】作图题:⊙O上有三个点A,B,C,∠BAC=70°,请画出要求的角,并标注.
(1)画一个140°的圆心角;(2)画一个110°的圆周角;(3)画一个20°的圆周角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=4,BC=8,∠ABC=60°.点P是边BC上一动点,作△PAB的外接圆⊙O交BD于E.
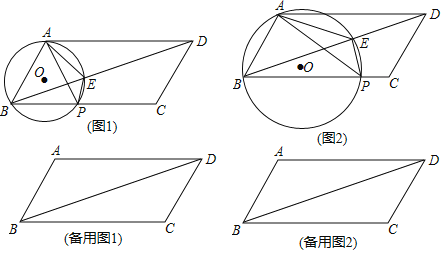
(1)如图1,当PB=3时,求PA的长以及⊙O的半径;
(2)如图2,当∠APB=2∠PBE时,求证:AE平分∠PAD;
(3)当AE与△ABD的某一条边垂直时,求所有满足条件的⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1 cm.参考数据: sin75°="0.966," cos75°=0.259,tan75°=3.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代城市绿化带在不断扩大,绿化用水的节约是一个非常重要的问题.


如图1、图2所示,某喷灌设备由一根高度为0.64 m的水管和一个旋转喷头组成,水管竖直安装在绿化带地面上,旋转喷头安装在水管顶部(水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计),旋转喷头可以向周围喷出多种抛物线形水柱,从而在绿化带上喷灌出一块圆形区域.现测得喷的最远的水柱在距离水管的水平距离3 m处达到最高,高度为1 m.
(1)求喷灌出的圆形区域的半径;
(2)在边长为16 m的正方形绿化带上固定安装三个该设备,喷灌区域可以完全覆盖该绿化带吗?如果可以,请说明理由;如果不可以,假设水管可以上下调整高度,求水管高度为多少时,喷灌区域恰好可以完全覆盖该绿化带.(以上需要画出示意图,并有必要的计算、推理过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com