
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.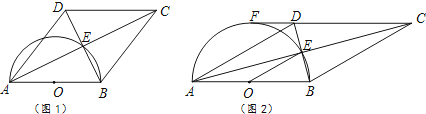
(1)利用图1,求证:四边形ABCD是菱形.
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
①连结OE,求△OBE的面积.
②求弧AE的长.
【答案】
(1)
证明:∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵AB为直径,且过点E,
∴∠AEB=90°,即AC⊥BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
(2)
证明:①连结OF.
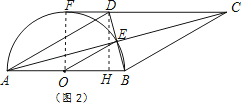
∵CD的延长线与半圆相切于点F,
∴OF⊥CF.
∵FC∥AB,
∴OF即为△ABD中AB边上的高.
∴S△ABD= ![]() AB×OF=
AB×OF= ![]() ×8×4=16,
×8×4=16,
∵点O是AB中点,点E是BD的中点,
∴S△OBE= ![]() S△ABD=4.
S△ABD=4.
②过点D作DH⊥AB于点H.
∵AB∥CD,OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°.
∴四边形OHDF为矩形,即DH=OF=4.
∵在Rt△DAH中,sin∠DAB= ![]() =
= ![]() ,
,
∴∠DAH=30°.
∵点O,E分别为AB,BD中点,
∴OE∥AD,
∴∠EOB=∠DAH=30°.
∴∠AOE=180°﹣∠EOB=150°.
∴弧AE的长= ![]() =
= ![]() .
.
【解析】(1)先由AE=EC、BE=ED可判定四边形为平行四边形,再根据∠AEB=90°可判定该平行四边形为菱形;(2)①连结OF,由切线可得OF为△ABD的高且OF=4,从而可得S△ABD , 由OE为△ABD的中位线可得S△OBE= ![]() S△ABD; ②作DH⊥AB于点H,结合①可知四边形OHDF为矩形,即DH=OF=4,根据sin∠DAB=
S△ABD; ②作DH⊥AB于点H,结合①可知四边形OHDF为矩形,即DH=OF=4,根据sin∠DAB= ![]() =
= ![]() 知∠EOB=∠DAH=30°,即∠AOE=150°,根据弧长公式可得答案本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.
知∠EOB=∠DAH=30°,即∠AOE=150°,根据弧长公式可得答案本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】已知正方形OABC的边长为2,顶点A,C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点,P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是以AP为腰的等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 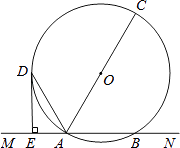
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
(1)请在数轴上标出点B和点C;
(2)求点B所表示的有理数与点C所表示的有理数的乘积;
(3)若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
北京时间 | 7:30 | 11:15 | 2:50 |
首尔时间 | 8:30 | 12:15 | 3:50 |
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )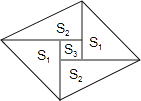
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
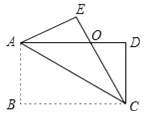
(1)求证:△AOE≌△COD;
(2)若∠OCD=30°,AB=![]() ,求△AOC的面积.
,求△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com