
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( ) 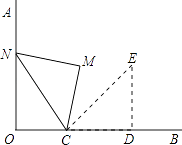
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上, ∴∠ECN=75°,
∵∠ECD=45°,
∴∠NCO=180°﹣75°﹣45°=60°,
∵AO⊥OB,
∴∠AOB=90°,
∴∠ONC=30°,
设OC=a,则CN=2a,
∵等腰直角三角形DCE旋转到△CMN,
∴△CMN也是等腰直角三角形,
设CM=MN=x,则由勾股定理得:x2+x2=(2a)2 ,
x= ![]() a,
a,
即CD=CM= ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() ,
,
故选C.
根据旋转得出∠NCE=75°,求出∠NCO,设OC=a,则CN=2a,根据△CMN也是等腰直角三角形设CM=MN=x,由勾股定理得出x2+x2=(2a)2 , 求出x= ![]() a,得出CD=
a,得出CD= ![]() a,代入求出即可.
a,代入求出即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图标信息回答下列问题: 体重频数分布表
组边 | 体重(千克) | 人数 |
A | 45≤x<50 | 12 |
B | 50≤x<55 | m |
C | 55≤x<60 | 80 |
D | 60≤x<65 | 40 |
E | 65≤x<70 | 16 |

(1)填空:①m=(直接写出结果); ②在扇形统计图中,C组所在扇形的圆心角的度数等于度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①abc>0;②方程ax2+bx+c=3有两个相等的实数根;③抛物线与x轴的另一个交点是(﹣1,0);④当1<x<4时,有y2>y1;⑤x(ax+b)≤a+b,其中正确的结论是 . (只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q. 
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图: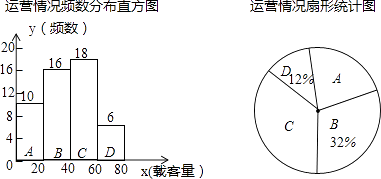
(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( ) 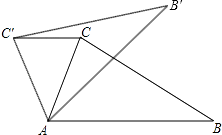
A.30°
B.35°
C.40°
D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com