
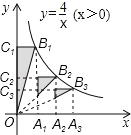
【题目】如图,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数![]() 的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
【答案】2![]() .
.
【解析】
试题分析:先根据反比例函数上的点向x轴、y轴引垂线形成的矩形面积等于反比例函数的|k|,得到S△OB1C1=S△OB2C2=S△OB3C3=![]() |k|=2,再根据相似三角形的面积比等于相似比的平方得到3个阴影部分的三角形的面积从而求得面积和.
|k|=2,再根据相似三角形的面积比等于相似比的平方得到3个阴影部分的三角形的面积从而求得面积和.
解:根据题意可知S△OB1C1=S△OB2C2=S△OB3C3=![]() |k|=2,
|k|=2,
∵OA1=A1A2=A2A3,A1B1∥A2B2∥A3B3∥y轴,
设图中阴影部分的面积从左向右依次为s1,s2,s3
则s1=![]() |k|=2,
|k|=2,
∵OA1=A1A2=A2A3,
∴s2:S△OB2C2=1:4,s3:S△OB3C3=1:9,
∴图中阴影部分的面积分别是s1=2,s2=![]() ,s3=
,s3=![]() ,
,
∴图中阴影部分的面积之和=2+![]() +
+![]() =2
=2![]() .
.
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
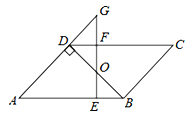
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
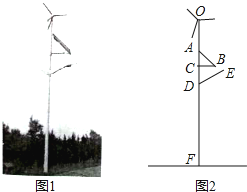
【题目】如图1,滨海广场装有风能、太阳能发电的风光互补环保路灯,灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°.AB=1.5米,CD=1米,为保证长为1米的风力发电机叶片无障碍安全旋转,对叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
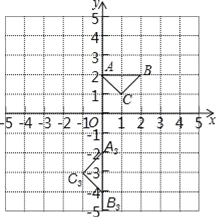
【题目】如图,平面直角坐标系中,已知A(0,2),B(2,2),C(1,1).
(1)将△ABC先向左平移2个单位长度,再向下平移1个单位长度,得到△A1B1C1,请画出△A1B1C1,点C1的坐标为______;
(2)将△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2,点C2的坐标为______;
(3)若将△ABC绕点P按顺时针方向旋转90°后得到△A3B3C3,则点P的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
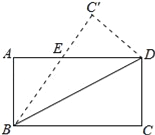
【题目】如图,在矩形ABCD中,BC=6cm,CD=3cm,将△BCD沿BD翻折,点C落在点C′处,BC′交AD于点E,则AE的长为______ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式3a2﹣9ab分解因式,正确的是( )
A. 3(a2﹣3ab) B. 3a(a﹣3b) C. a(3a﹣9b) D. a(9b﹣3a)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com