
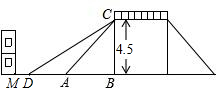
 如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)
如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上) 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 折纸三等分角 三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一(三等分任意角、化圆为方、倍立方),即用圆规与直尺(没有刻度,只能做直线的尺子)把一任意角三等分,这问题曾吸引着许多人去研究,但无一成功.1837年法国数学家凡齐尔(1814~1848)运用代数方法证明了,仅用尺规不可鞥呢三等分角. 如果作图工具没有限制,将条件放宽,将任意角三等分是可以解决的.下面介绍一种折纸三等分任意锐角的方法: (1)在正方形纸片上折出任意∠SBC,将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,得到图(1); (2)翻折左下角使点B与EF上的点T重合,点M与SB上的点P重合,点E对折后的对应点记为Q,折痕为记为GH,得到图(2); (3)折出射线BQ,BT,得到图(3),则射线BQ,BT就是∠SBC的三等分线.  下面是证明BQ,BT是∠SBC三等分线的部分过程: 证明:过T作TK⊥BC,垂足为K,则四边形EBKT为矩形 根据折叠,得EB=QT,∠EBT=∠QTB,BT=TB ∴△EBT≌△QTB, ∴∠BQT=∠TEB=90°, ∴BQ⊥PT … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ABC=90°,AB是⊙O的直径,连接OC,过点A作AD∥OC交⊙O于点D,连接CD.
如图,在Rt△ABC中,∠ABC=90°,AB是⊙O的直径,连接OC,过点A作AD∥OC交⊙O于点D,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AD=2,AB=3,点E是AD边的中点,点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A′EF,连接A′C,则A′C的最小值为$\sqrt{10}$-1.
如图,在矩形ABCD中,AD=2,AB=3,点E是AD边的中点,点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A′EF,连接A′C,则A′C的最小值为$\sqrt{10}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com