【题目】如图1和图2，
是直线
上一动点，
两点在直线的同侧，且点所在直线与不平行.
（1）当点运动到
位置时，距离
点最近，在图1中的直线上画出点的位置；
（2）当点运动到
位置时，与点的距离和与
点距两相等，请在图2中作出位置；
（3）在直线上是否存在这样一点
，使得到点的距离与到点的距离之和最小？若存在请在图3中作出这点，若不存在清说明理由.
（要求：不写作法，请保留作图痕迹）
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案科目：初中数学 来源： 题型：
【题目】为响应市政府“绿色出行”的号召，小张上班由自驾车改为骑公共自行车．已知小张家距上班地点10千米．他骑公共自行车比自驾车平均每小时少行驶45千米，他从家出发到上班地点，骑公共自行车所用的时间是自驾车所用的时间的4倍．小张骑公共自行车平均每小时行驶多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，BC=a ，AB=c，AC=b，则不能作为判定△ABC是直角三角形的条件的是（ ）
A.
B.∠A∶∠B∶∠C=1∶4∶3
C.a∶b∶c =7∶24∶25D.a∶b∶c =4∶5∶6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，
，
．动点
、
分别从点
、点
同时出发，相向而行，速度都为
．以
为一边向上作正方形
，过点作
，交
于点
．设运动时间为
，单位：
，正方形和梯形
重合部分的面积为
．
当
时，点与点重合．
当时，点
在
上．
当点在，两点之间（不包括，两点）时，求
与
之间的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
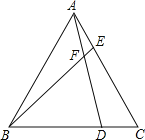
【题目】 如图，已知△ABC为等边三角形，D、E分别为BC、AC边上的两动点（与点A、B、C不重合），且总使CD = AE，AD与BE相交于点F．
（1）求证：AD = BE；
（2）求∠BFD的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下面的内容，再解答问题．
（阅读）例题：求多项式m2 + 2mn+2n2-6n+13的最小值．
解；m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4，
∵(m+n)2
0, (n-3)20
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
（解答问题）
（1）请写出例题解答过程中因式分解运用的公式是
（2）己知a、b、c是△ABC的三边，且满足a2+b2=l0a+8b-41，求第三边c的取值范围；
（3）求多项式－2x2＋4xy－3y2 －3y2－6y＋7 的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙D的直径，AD切⊙D于点A，EC=CB．则下列结论：①BA⊥DA；②OC∥AE；③∠COE=2∠CAE；④OD⊥AC．一定正确的个数有（ ）
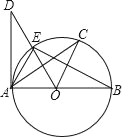
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
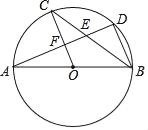
【题目】如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD与BC，OC分别相交于点E，F，则下列结论：①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤△CEF≌△BED．其中一定成立的结论是_____．（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（－3，5），B（－2，1），C（－1，3）．
（1）画出△ABC关于x轴的对称图形△A1B1C1；
（2）画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2；
（3）如果AC上有一点M（a，b）经过上述两次变换，那么对应A2C2上的点M2的坐标是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
