
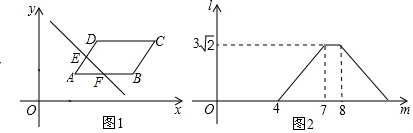
分析 根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,当直线经过D点,则DF=3$\sqrt{2}$,作DM⊥AB于点M.利用三角函数即可求得DM即平行四边形的高,然后利用平行四边形的面积公式即可求解.
解答  解:根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,
解:根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,
则AB=8-4=4,
当直线经过D点,则DF=3$\sqrt{2}$,作DM⊥AB于点M.
∵y=-x与x轴形成的角是45°,
又∵AB∥x轴,
∴∠DFM=45°,
∴DM=DF•sin45°=3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=3,
则平行四边形的面积是:AB•DM=4×3=12,
故答案为:12.
点评 本题考查了函数的图象,根据图象理解AB的长度,正确求得平行四边形的高是关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
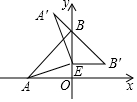 如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.
如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com