
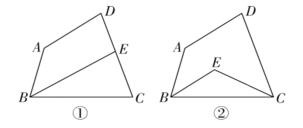
【题目】如图,在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(2)如图②,若∠ABC和∠BCD的平分线交于点E,试求出∠BEC的度数.
【答案】(1)60°;(2)110°
【解析】
(1)根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,进一步根据四边形的内角和定理进行求解;
(2)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB的度数,再进一步求得∠BEC的度数.
解: (1)∵BE∥AD,
∴∠A+∠ABE=180°,
即140°+∠ABE=180°.
∴∠ABE=40°.
∴∠ABC=80°.
∵∠A+∠ABC+∠C+∠D=360°,
∴∠C=360°-140°-80°-80°=60°.
(2)∵∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD,
∠BCD,
由∠A+∠ABC+∠BCD+∠D=360°,
得140°+2∠EBC+2∠ECB+80°=360°.
∴∠EBC+∠ECB=70°.
∴∠BEC=180°-70°=110°.


科目:初中数学 来源: 题型:
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
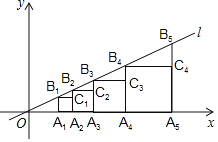
【题目】如图,已知直线l:y=![]() x,点A1(2,0),过点A1作x轴的垂线交直线l于点B1,以A1B1为边,向右侧作正方形A1B1C1A2,延长A2C1交直线l于点B2;以A2B2为边,向右侧作正方形A2B2C2A3,延长A3C2交直线l于点B3;以A3B3为边,向右侧作正方形A3B3C3A4,延长A4C3交直线l于点B4;…;按照这个规律继续作下去,点Bn的横坐标为_.(结果用含正整数n的代数式表示)
x,点A1(2,0),过点A1作x轴的垂线交直线l于点B1,以A1B1为边,向右侧作正方形A1B1C1A2,延长A2C1交直线l于点B2;以A2B2为边,向右侧作正方形A2B2C2A3,延长A3C2交直线l于点B3;以A3B3为边,向右侧作正方形A3B3C3A4,延长A4C3交直线l于点B4;…;按照这个规律继续作下去,点Bn的横坐标为_.(结果用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动会中裁判员使用的某品牌遮阳伞如图1所示,图2是其剖面图,若AG平分∠BAC与∠EDF,AB∥ED,求证:AC∥DF.
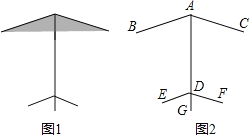
请将横线上的证明过程和依据的定理补充完整.
证明:∵AB∥DE,
∴∠ =∠ ( )
∵AG平分∠BAC,AG平分∠EDF(已知)
∴∠DAC=∠DAB,∠GDF=∠GDE( ).
∴∠DAC=∠GDF( ).
∴AC∥DF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
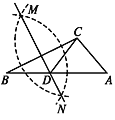
【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于![]() BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
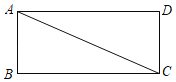
【题目】如图,有一个长方形花园,对角线AC是一条小路,现要在AD边上找一个位置建报亭H,使报亭H到小路两端点A、C的距离相等.
(1)用尺规作图的方法,在图中找出报亭H的位置(不写作法,但需保留作图痕迹,交代作图结果)
(2)如果AD=80m,CD=40m,求报亭H到小路端点A的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com