练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，AB是圆O的直径，弦CD⊥AB，垂足为E，若AB=10，CD=8，则AE=
    2
    2
    ．
    分析：由CD的长根据垂径定理可知CE的长，利用勾股定理可将弦心距OE的长求出，进而可求出AE的长．
    解答：解：如图，连接OC．
    ∵弦CD⊥AB于E，CD=8，∴CE=4．
    ∵AB=10，∴OC=
    1
    2
    AB=5．
    在Rt△OCE中，CE2+OE2=OC2，即：42+OE2=52
    解得：OE=3，
    ∴AE=OA-OE=2．
    故答案是：2．
    点评：本题综合考查了垂径定理和勾股定理的求法及性质．此类在圆中涉及弦长、半径的计算的问题，常把半弦长，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系内，以y轴为对称轴的抛物线经过直y=-
    		3
    3
    x+2与y轴的交点A和点M（-
    		3
    2
    ，0）．
    （1）求这条抛物线所对应的二次函数的关系式；
    （2）将（1）中所求抛物线沿x轴向右平移．①在题目所给的图中画出沿x轴平移后经过原点的抛物线大致图象；②设沿x轴向右平移后经过原点的抛物线对称轴与直线AB相交于C点．判断以O为圆心，OC为半径的圆与直线AB的位置关系，并说明理由；
    （3）P点是沿x轴向右平移后经过原点的抛物线对称轴上的点，求P点的坐标，使得以O，A，C，P四点为顶点的精英家教网四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（35）：2.7 最大面积是多少（解析版） 题型：解答题

    如图，在平面直角坐标系内，以y轴为对称轴的抛物线经过直y=-x+2与y轴的交点A和点M（-，0）．
    （1）求这条抛物线所对应的二次函数的关系式；
    （2）将（1）中所求抛物线沿x轴向右平移．①在题目所给的图中画出沿x轴平移后经过原点的抛物线大致图象；②设沿x轴向右平移后经过原点的抛物线对称轴与直线AB相交于C点．判断以O为圆心，OC为半径的圆与直线AB的位置关系，并说明理由；
    （3）P点是沿x轴向右平移后经过原点的抛物线对称轴上的点，求P点的坐标，使得以O，A，C，P四点为顶点的四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源：第6章《二次函数》中考题集（38）：6.4 二次函数的应用（解析版） 题型：解答题

    如图，在平面直角坐标系内，以y轴为对称轴的抛物线经过直y=-x+2与y轴的交点A和点M（-，0）．
    （1）求这条抛物线所对应的二次函数的关系式；
    （2）将（1）中所求抛物线沿x轴向右平移．①在题目所给的图中画出沿x轴平移后经过原点的抛物线大致图象；②设沿x轴向右平移后经过原点的抛物线对称轴与直线AB相交于C点．判断以O为圆心，OC为半径的圆与直线AB的位置关系，并说明理由；
    （3）P点是沿x轴向右平移后经过原点的抛物线对称轴上的点，求P点的坐标，使得以O，A，C，P四点为顶点的四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源：第27章《二次函数》中考题集（37）：27.3 实践与探索（解析版） 题型：解答题

    如图，在平面直角坐标系内，以y轴为对称轴的抛物线经过直y=-x+2与y轴的交点A和点M（-，0）．
    （1）求这条抛物线所对应的二次函数的关系式；
    （2）将（1）中所求抛物线沿x轴向右平移．①在题目所给的图中画出沿x轴平移后经过原点的抛物线大致图象；②设沿x轴向右平移后经过原点的抛物线对称轴与直线AB相交于C点．判断以O为圆心，OC为半径的圆与直线AB的位置关系，并说明理由；
    （3）P点是沿x轴向右平移后经过原点的抛物线对称轴上的点，求P点的坐标，使得以O，A，C，P四点为顶点的四边形是平行四边形．

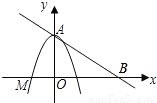
    查看答案和解析>>

    科目：初中数学 来源：2008年四川省眉山市中考数学试卷（解析版） 题型：解答题

    （2008•眉山）如图，在平面直角坐标系内，以y轴为对称轴的抛物线经过直y=-x+2与y轴的交点A和点M（-，0）．
    （1）求这条抛物线所对应的二次函数的关系式；
    （2）将（1）中所求抛物线沿x轴向右平移．①在题目所给的图中画出沿x轴平移后经过原点的抛物线大致图象；②设沿x轴向右平移后经过原点的抛物线对称轴与直线AB相交于C点．判断以O为圆心，OC为半径的圆与直线AB的位置关系，并说明理由；
    （3）P点是沿x轴向右平移后经过原点的抛物线对称轴上的点，求P点的坐标，使得以O，A，C，P四点为顶点的四边形是平行四边形．

    查看答案和解析>>

    同步练习册答案