
 如图,E是正方形ABCD中CD边上一点,以点A为中心把△ADE顺时针旋转90°.
如图,E是正方形ABCD中CD边上一点,以点A为中心把△ADE顺时针旋转90°.分析 (1)在CB的延长线上截取BM=DE,则△ABM满足条件;
(2))①由旋转性质得AM=AE,∠MAE=90°,则∠MAF=∠EAF=45°,则可根据“SAS”判断△AMF≌△AEF;
②由△AMF≌△AEF得到EF=MF,即ME=BF+MB,加上BM=DE,所以EF=BF+DE,再利用勾股定理计算出DE=3,则CE=3,设EF=x,则BF=x-3,CF=9-x,然后在Rt△CEF中利用勾股定理得到(9-x)2+32=x2,然后解方程求出x即可.
解答 (1)解:如图,△ABM为所作;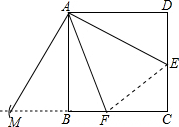
(2)①证明:∵ABCD 是正方形,
∴∠BAD=90°,
∵△ADE绕点A顺时针旋转90°得到△ABM,
∴AM=AE,∠MAE=90°,
又∵∠EAF=45°,
∴∠MAF=45°,
∴∠MAF=∠EAF,
在△AMF和△AEF中
$\left\{\begin{array}{l}{AM=AE}\\{∠MAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△AMF≌△AEF;
②解:∵△AMF≌△AEF,
∴EF=MF,
即ME=BF+MB,
而BM=DE,
∴EF=BF+DE,
在Rt△ADE中,DE=$\sqrt{(3\sqrt{5})^{2}-{6}^{2}}$=3,
∴CE=6-3=3,
设EF=x,则BF=x-3,
∴CF=6-(x-3)=9-x,
在Rt△CEF中,∵CF2+CE2=EF2,
∴(9-x)2+32=x2,解得x=5,
解EF=5.
故答案为5.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了正方形的性质和全等三角形的判定与性质.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王老师获得一张2016宝应春节联欢晚会的门票,想奖给班级学校优秀的同学,通过考察,小明和小刚脱颖而出,但问题是只有一张门票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看晚会,他们各自提出了一个方案:
王老师获得一张2016宝应春节联欢晚会的门票,想奖给班级学校优秀的同学,通过考察,小明和小刚脱颖而出,但问题是只有一张门票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看晚会,他们各自提出了一个方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
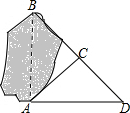 如图,为了测量出池塘两端A、B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BD至D,使CD=BC,那么只要测量出AD的长度就得到A,B两点之间的距离,你能说明其中的道理吗?
如图,为了测量出池塘两端A、B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BD至D,使CD=BC,那么只要测量出AD的长度就得到A,B两点之间的距离,你能说明其中的道理吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
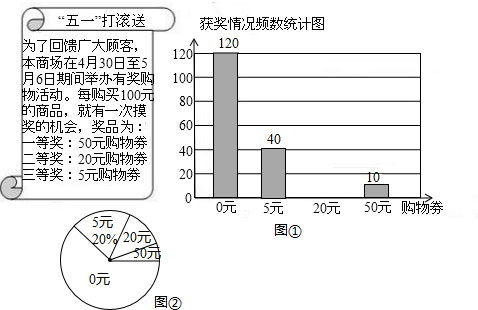
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
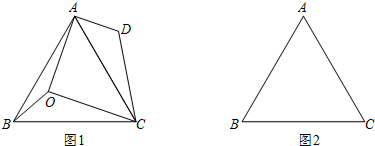
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com