
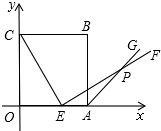
 如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.分析 (1)在OC上截取OK=OE.连接EK,求出∠KCE=∠CEA,根据ASA推出△CKE≌△EAP,根据全等三角形的性质得出即可;
(2)过点B作BM∥PE交y轴于点M,根据ASA推出△BCM≌△COE,根据全等三角形的性质得出BM=CE,求出BM=EP.根据平行四边形的判定得出四边形BMEP是平行四边形,即可求出答案.
解答 (1)证明:在OC上截取OK=OE.连接EK,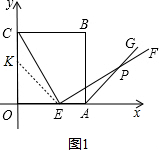
∵OC=OA,∠COA=∠BA0=90°,∠OEK=∠OKE=45°,
∵AP为正方形OCBA的外角平分线,
∴∠BAP=45°,
∴∠EKC=∠PAE=135°,
∴CK=EA,
∵EC⊥EP,
∴∠CEF=∠COE=90°,
∴∠CEO+∠KCE=90°,∠CEO+∠PEA=90°,
∴∠KCE=∠CEA,
在△CKE和△EAP中
$\left\{\begin{array}{l}{∠KCE=∠PEA}\\{CK=EA}\\{∠CKE=∠EAP}\end{array}\right.$
∴△CKE≌△EAP,
∴EC=EP;
(2)解:y轴上存在点M,使得四边形BMEP是平行四边形.
如图,过点B作BM∥PE交y轴于点M,连接BP,EM,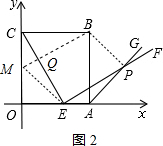
则∠CQB=∠CEP=90°,
所以∠OCE=∠CBQ,
∵在△BCM和△COE中,$\left\{\begin{array}{l}{∠CBM=∠OCE}\\{BC=OC}\\{∠BCM=∠COE}\end{array}\right.$
∴△BCM≌△COE,
∴BM=CE,
∵CE=EP,
∴BM=EP.
∵BM∥EP,
∴四边形BMEP是平行四边形,
∵△BCM≌△COE,
∴CM=OE=3,
∴OM=CO-CM=2.
故点M的坐标为(0,2).
点评 本题考查了正方形的性质,全等三角形的性质和判定,平行四边形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键,综合性比较强,难度偏大.


科目:初中数学 来源: 题型:选择题
| A. | 2≤a≤3 | B. | 2<a≤3 | C. | 2≤a<3 | D. | 2<a<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
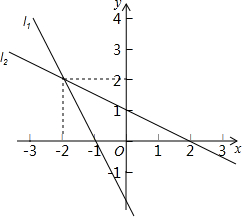 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某品牌钢笔的使用寿命 | |
| B. | 了解某市学生的视力情况 | |
| C. | 调查乘坐飞机的乘客是否携带违禁物品 | |
| D. | 了解某市学生课外阅读情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-3(x+4)+1 | B. | y=-(x-4)+1 | C. | y=-3x+5 | D. | y=-3x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码/cm | 21.5 | 22.0 | 22.5 | 23.0 | 23.5 |
| 人数 | 2 | 4 | 3 | 8 | 3 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com