
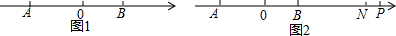
���� ��1�����÷Ǹ������������a��b��ֵ������ȷ����AB�ij���
��2�������֪���̵Ľ�ȷ����x���õ�C��ʾ�ĵ㣬���P�������϶�Ӧ������m����PA+PB=$\frac{1}{4}$BC+ABȷ����Pλ�ã����������жϣ�
��3����P������ʾ����Ϊn������PA=n+6��PB=n-4�����������Ϳ��Ա�ʾ��PM=$\frac{n+6}{2}$��BN=$\frac{2}{3}$����n-4�����ٷֱ�����$\frac{1}{2}$PM-$\frac{3}{8}$BN�͢�PM+$\frac{3}{4}$BN�����ֵ���ɣ�
��� �⣺��1����|a+6|+��b-4��2=0��
��a+6=0��b-4=0��
��a=-6��b=4��
��AB=|-6-4|=10��
��AB�ij�Ϊ10��
��2�������ڣ�
��2x+1=$\frac{1}{4}$x-5��
��x=-8��
��BC=12��
���P�������϶�Ӧ������m��
��PA+PB=$\frac{1}{4}$BC+AB��
��|m+6|+|m-4|=$\frac{1}{4}$��12+3��
��m+6=0��m-4=0��
��m=-6��m=4��
�ٵ�m��-6ʱ��
-m-6+4-m=13��
m=-7.5��
�ڵ�-6��m��4ʱ��
m+6+4-m=13������ȥ����
�۵�m��4ʱ��
m+6+m-4=13��
m=5.5��
�൱��P��ʾ����Ϊ-7.5��5.5ʱ��PA+PB=$\frac{1}{4}$BC+AB��
��3����P������ʾ����Ϊn��
��PA=n+6��PB=n-4��
��PA���е�ΪM��
��PM=$\frac{1}{2}$PA=$\frac{n+6}{2}$��
NΪPB�����ȷֵ��ҿ�����P�㣬
��BN=$\frac{2}{3}$PB=$\frac{2}{3}$����n-4����
���$\frac{1}{2}$PM-$\frac{3}{8}$BN=$\frac{1}{2}$��$\frac{n+6}{2}$-$\frac{3}{8}$��$\frac{2��n-4��}{3}$=$\frac{5}{2}$�����䣩��
��PM+$\frac{3}{4}$BN=$\frac{n+6}{2}$+$\frac{3}{4}$��$\frac{2��n-4��}{3}$=n+1�����P�ı仯���仯����
����ȷ�Ľ���Ϊ��$\frac{1}{2}$PM-$\frac{3}{8}$BN��ֵ���䣬��ֵΪ$\frac{5}{2}$��
���� ���⿼����һԪһ�η��̵����ã��ֶκ��������ã���������ã����������������ľ��빫ʽ�����ã�ȥ����ֵ�����ã����ʱ��������������ľ��빫ʽ����ǹؼ���


 Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{9}$S | B�� | $\frac{1}{6}$S | C�� | $\frac{1}{4}$S | D�� | $\frac{1}{3}$S |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
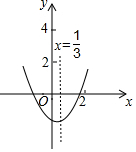 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���c��0����abc��0����a-b+c��0����2a-3b=0����c-4b��0��������ȷ���۵ĸ����У�������
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���c��0����abc��0����a-b+c��0����2a-3b=0����c-4b��0��������ȷ���۵ĸ����У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��-2 | B�� | 4��1 | C�� | 2��1 | D�� | 4��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2��x��0 | C�� | x��2 | D�� | x��2��x��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
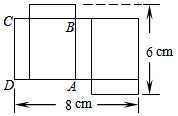 ��ͼ��һ��������ı���չ��ͼ���ı���ABCD�������Σ������ͼ�����ݿɵ�ԭ������������12cm3��
��ͼ��һ��������ı���չ��ͼ���ı���ABCD�������Σ������ͼ�����ݿɵ�ԭ������������12cm3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������a��b��c�������ϵ�λ����ͼ��ʾ������|a+c|-|a-b|+|b+c|-|b|��
������a��b��c�������ϵ�λ����ͼ��ʾ������|a+c|-|a-b|+|b+c|-|b|���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com