
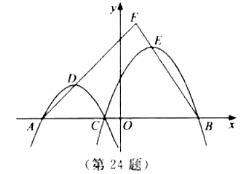
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点(与
上一点(与![]() ,
,![]() 点不重合),抛物线
点不重合),抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,抛物线
,抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,
,![]() ,
,![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)若![]() ,
,![]() ,求抛物线
,求抛物线![]() ,
,![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)是否存在这样的实数![]() (
(![]() ),无论
),无论![]() 取何值,直线
取何值,直线![]() 与
与![]() 都不可能互相垂直?若存在,请直接写出
都不可能互相垂直?若存在,请直接写出![]() 的两个不同的值;若不存在,请说明理由.
的两个不同的值;若不存在,请说明理由.
【答案】(1)抛物线L1的解析式为y=![]() ,抛物线L2的解析式为y=
,抛物线L2的解析式为y=![]() (2)m=±2
(2)m=±2![]() (3)存在
(3)存在
【解析】
试题分析:(1)把a、m代入得到已知点,把点代入函数的解析式,然后构成方程组,根据待定系数法可求出函数的解析式;
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H,把a=-1代入函数解析式,然后结合(m,0)和(-4,0)代入可求解出函数解析式L1,然后分别求出D点坐标,得到DG、AG的长,同理得到L2,求得EH,BH的长,再根据三角形相似的判定与性质构造方程求解即可;
(3)根据前面的解答,直接写出即可.
试题解析:(1)由题意得
解得
所以抛物线L1的解析式为y=![]()
同理,
解得
∴所以抛物线L2的解析式为y=![]()
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H
由题意得
解得
∴抛物线L1的解析式为y=-x2+(m-4)x+4m
∴点D的坐标为(![]() ,
,![]() )
)
∴DG=![]() ,AG=
,AG=![]()
同理可得,抛物线L2的解析式为y=-x2+(m+4)x-4m
EH=![]() ,BH=
,BH=![]()

∵AF⊥BF,DG⊥x轴,EH⊥x轴
∴∠AFB=∠AGD=∠EHB=90°
∴∠ADG=∠ABF=90°-∠BAF
∴△ADG∽△EBH
∴![]()
∴
解得m=±2![]()
(3)存在,例如:a=-![]() ,a=-
,a=-![]() .(答案不唯一)
.(答案不唯一)


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义一种新运算“*”,规定a*b=ab+a﹣b,如1*3=1×3+1﹣3,则﹣2*5等于( )
A. 17B. 15C. ﹣17D. ﹣15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)如图1,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A.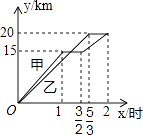
B.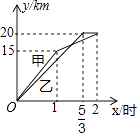
C.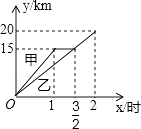
D.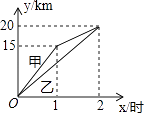
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+3与y轴交于点A,直线y=kx﹣1与y轴交于点B,与直线y=2x+3交于点C(﹣1,n).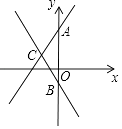
(1)求n、k的值;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com