
分析 如图,△ABC为⊙O的内接正三角形,作AD⊥BC于D,则BD=CD,根据垂径定理的推论可得圆心O在AD上,连接OB,如图,利用圆的面积公式计算出圆的半径为$\sqrt{3}$,根据等边三角形的性质可判断点O为等边△ABC的外心和内心,则∠OBD=$\frac{1}{2}$∠ABD=30°,接着根据含30度的直角三角形三边的关系计算出OD=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{2}$,BD=$\sqrt{3}$OD=$\frac{3}{2}$,然后根据三角形面积公式求解.
解答  解:如图,△ABC为⊙O的内接正三角形,
解:如图,△ABC为⊙O的内接正三角形,
作AD⊥BC于D,则BD=CD,
∴圆心O在AD上,
连接OB,如图,设⊙O的半径为r,
∵⊙O的面积为3π,
∴πr2=3π,解得r=$\sqrt{3}$,
∵点O为等边△ABC的外心,
∴点O为等边△ABC的内心,
∴∠OBD=$\frac{1}{2}$∠ABD=30°,
在Rt△OBD中,OD=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{2}$,
BD=$\sqrt{3}$OD=$\frac{3}{2}$,
∴BC=2BD=3,
∴S△ABC=$\frac{1}{2}$AD•BC=$\frac{1}{2}$×($\sqrt{3}$+$\frac{\sqrt{3}}{2}$)×3=$\frac{9\sqrt{3}}{4}$.
故答案为:$\frac{9\sqrt{3}}{4}$.
点评 本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.解决本题的关键是等边三角形性质的灵活应用.


科目:初中数学 来源: 题型:解答题
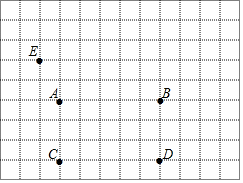 某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).
某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
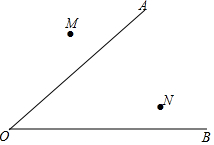 用直尺和圆规作图:(不写作法,保留作图痕迹)
用直尺和圆规作图:(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com