
 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.分析 (1)连接OQ,在Rt△OPQ中,利用勾股定理即可解决问题.
(2)如图2中,过点O作OC⊥AB于C.只要证明△PBA∽△PQO,即可推出∠PBA=∠PQO=90°.
(3)首先证明四边形OCBQ是矩形,分两种情形列出方程即可解决问题.
解答 解:(1)如图1中,连接OQ,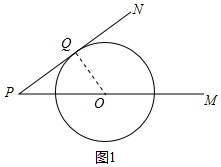
∵PN与⊙O相切于点Q,
∴OQ⊥PN,
∴∠OQP=90°,
∵OQ=6cm,OP=10cm,
∴PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
(2)如图2中,过点O作OC⊥AB于C.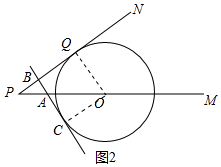
由题意,PA=5t,PB=4t,
∵OP=10,PQ=8,
∴$\frac{PA}{PO}$=$\frac{PB}{PQ}$,∵∠P=∠P,
∴△PBA∽△PQO,
∴∠PBA=∠PQO=90°,
∴AB⊥PN.
(3)∵∠BQO=∠CBQ=∠OCB=90°,
∴四边形OCBQ是矩形,
∴BQ=OC=6,
∵OC=6cm,
∴BQ=6cm.
①当AB运动到图2位置时,BQ=PQ-PB=6,
∴8-4t=6,
∴t=0.5s,
②当AB运动到图3位置时,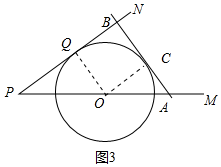
BQ=AB-PQ=6,
∴4t-8=6,
∴t=3.5s,
综上所述,t=0.5s或3.5s时,直线AB与⊙O相切.
点评 本题考查圆的综合题、勾股定理.相似三角形的判定和性质、矩形的性质和判定、切线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.


科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:判断题
一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆成如下右图形式,使点B、F、C、D在同一条直线上.
(1)求证AB⊥ED;
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 利用平面直角坐标系求抛物线y=x2-4x+3与坐标轴的交点围成的△ABC的周长和面积.抛物线上是否存在点D,使△ABD与△ABC面积相等,如果有,请写出D点坐标.
利用平面直角坐标系求抛物线y=x2-4x+3与坐标轴的交点围成的△ABC的周长和面积.抛物线上是否存在点D,使△ABD与△ABC面积相等,如果有,请写出D点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
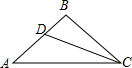 如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
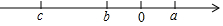 已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(1,2) | B. | y的值随x值的增大而减小 | ||
| C. | 图象在第一、三象限内 | D. | 若x>1,则0<y<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com