
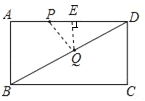
����Ŀ����ͼ���ھ���ABCD�У�AB��6��BC��8������P�ڱ�AD����ÿ��2����λ���ٶȴ�A��������AD��D�˶���ͬʱ����Q�ڱ�BD����ÿ��5����λ���ٶȴ�D��������DB��B�˶�����������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮
��1����գ���ijһʱ��t��ʹ��t��1ʱ��P��Q�����ľ���PQ���� ����
��2���Ƿ������P��D��Q��һ��ΪԲ�ĵ�Բǡ�ù����������㣿�����������ʱt��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��![]() ����2�����ڣ�t��ֵΪ
����2�����ڣ�t��ֵΪ![]() s��
s��![]() s��
s��![]() s��
s��
��������
��1�����ݾ��ε����ʵõ���BAD��90�������ݹ��ɶ����õ�BD��10����Q��QE��AD��E�����������ε���λ�ߵ����ʵõ�EQ��![]() AB��3��PE��2�����ݹ��ɶ������ɵõ����ۣ�
AB��3��PE��2�����ݹ��ɶ������ɵõ����ۣ�
��2��������õ�AP��2t��DQ��5t��PD��8��2t������ƽ���߷��߶γɱ��������õ�QE��3t�����ݹ��ɶ����õ�PQ��![]() ����D��Բ��ʱ��PD��DQ����P��Բ��ʱ��PD��PQ����Q��Բ��ʱ��PQ��DQ���з��̼��ɵõ����ۣ�
����D��Բ��ʱ��PD��DQ����P��Բ��ʱ��PD��PQ����Q��Բ��ʱ��PQ��DQ���з��̼��ɵõ����ۣ�
��1����t��1��
��AP��2��DQ��5��
��PD��6��
���ı���ABCD�Ǿ��Σ�
����BAD��90�㣬
��AB��6��BC��8��
��BD��10��
��QΪBD���е㣬
��Q��QE��AD��E��
��QE��AB��
��AE��DE��4��
��EQ��![]() AB��3��PE��2��
AB��3��PE��2��
��PQ��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2�����ڣ�
���ɣ���AP��2t��DQ��5t��
��PD��8��2t��
�ɣ�1��֪��QE��AB��
��![]() ��
��
��![]() ��
��
��QE��3t��
��DE��4t��
��PE��8��6t��
��PQ��![]() ��
��
��D��Բ��ʱ��PD��DQ��
��8��2t��5t��
��ã�t��![]() ��
��
��P��Բ��ʱ��PD��PQ��
��8��2t��![]() ��
��
��ã�t��![]() ����t��0����ȥ����
����t��0����ȥ����
��Q��Բ��ʱ��PQ��DQ��
��5t��![]() ��
��
��ã�t��![]() ��t��4����ȥ����
��t��4����ȥ����
����������t��ֵΪ![]() s��
s��![]() s��
s��![]() s��
s��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
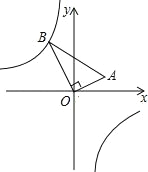
����Ŀ����ͼ���ڡ�AOB�У���AOB��90�㣬��A������Ϊ��4��2����BO��4![]() ������������y��
������������y��![]() ��ͼ����B����k��ֵΪ_____��
��ͼ����B����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ƽ�С�����ò���Χ��һ�����Ϊ60��2�ľ��οƼ�ABCD������һ��AB��ǽ��ǽ��Ϊ12������AD�ij�Ϊ������DC�ij�Ϊ������
��1��������֮��ĺ�����ϵʽ��
��2����Χ�ɾ��οƼ�ABCD�����߲����ܳ�������26��������AD��DC�ij������������������������������Χ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ʵ�������ϵ�����ú���֪ʶ�����������⣺
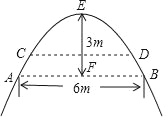
��ͼ����ij�����ϵ�һ���������ι��ţ����Ŷ�����E������ˮ��ľ���EFΪ3��ʱ��ˮ���ABΪ6�ף�һ���������ˮ���ǣ�ˮ����ȱ�ΪCD����CD=2![]() �ף���ʱˮλ�����˶����ף�
�ף���ʱˮλ�����˶����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ�ˡ�չ�����۵�����һ�κ������˺ܶ༸���嶼��չ����ƽ��ͼ�Σ��������ڼ��ü���չ����һ��������ֽ�У�����һ��С�Ķ����һ���⣬��ֽ�м����������֣���ͼ�еĢٺ͢ڣ���������ѧ��֪ʶ���ش��������⣺

��1��С���ܹ�������_______���⣮
��2������С���뽫���ϵĢ�����ճ��������ȥ�����Ҿ����۵��Ժ���Ȼ���Ի�ԭ��һ��������ֽ�У�����Ϊ��Ӧ�ý����ϵ�ֽ��ճ�������е�ʲôλ�ã��������С���ڢ��ϲ�ȫ��
��3��С��˵�����������������У����һ��������̵�һ�����5����������֪���������ֽ�еĵ�����һ�������Σ��������������ֽ�������ⳤ�ĺ���880cm�������������ֽ�е������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±���

��һԪ���η���x2-2x-2=0�ھ�ȷ��0.1ʱһ�����Ƹ���______�����������ߵĶԳ��ԣ�����֪�÷��̵���һ�����Ƹ���_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ�νֵ�������������ֱ�߷ֱ�ΪAB��PQ������AB��PQ���������һ��DE���ڵ�ֱ��MN��AB�ڵ�M����PQ�ڵ�N��С����ʤ���ֵ�A��������AB����ǰ����С��һֱվ�ڵ�P��λ�õȴ�С����
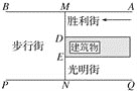
(1)���㻭��С��ǡ���ܿ���С�������ߣ��Լ���ʱС�����ڵ�λ��(�õ�C���)��
(2)��֪��MN��30 m��MD��12 m��PN��36 m����(1)�еĵ�C��ʤ���ֿڵľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCDEF��������GHIJKL�����Ʊ�Ϊ2��1�������н�����ȷ���ǣ� ��

A. ��E=2��K B. BC=2HI C. ������ABCDEF���ܳ�=������GHIJKL���ܳ� D. S������ABCDEF=2S������GHIJKL
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A�Ƿ���������y��![]() ��x��0����ͼ���ϵ�һ�����㣬����OA��OB��OA����OB��2OA����ô������B�ķ���������ͼ��ı���ʽΪ��������
��x��0����ͼ���ϵ�һ�����㣬����OA��OB��OA����OB��2OA����ô������B�ķ���������ͼ��ı���ʽΪ��������
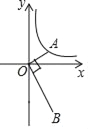
A. y����![]() B. y��
B. y��![]() C. y����
C. y����![]() D. y��
D. y��![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com