
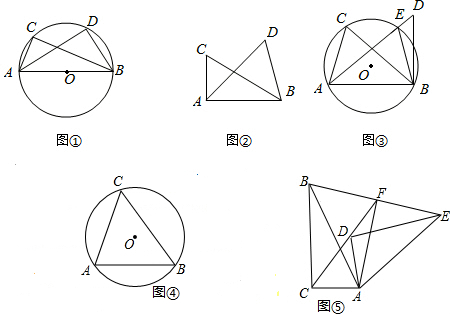
分析 [思考]运用反证法,假设点D在圆内,根据圆周角定理和三角形的外角的性质证明与已知∠ACB=∠ADB相矛盾即可;
[应用](1)根据等腰三角形的性质、圆周角定理得到∠ACD=∠ABE,即可得到结论;
(2)由B、C、A、F四点共圆,得到∠BFA+∠BCA=180°,推出AF⊥BE,根据等腰三角形的性质即可得到结论.
解答 [思考]证明:如图,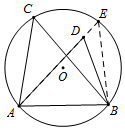
假设点D在⊙O内,延长AD交⊙O于点E,连接BE;
则∠AEB=∠ACB,
∵∠ADB是△DBE的一个外角,
∴∠ADB>∠AEB,
∴∠ADB>∠ACB,
这与条件∠ACB=∠ADB矛盾,
∴点D不在⊙O内;
[应用]证明:(1)∵AC=AD,AB=AE,
∴∠ACD=∠ADC,∠ABE=∠AEB,
∵∠CAB=∠DAE,
∴∠CAD=∠BAE,
∵2∠ACD+∠CAD=180°,2∠ABE+∠BAE=180°,
∴∠ACD=∠ABE,
∴B、C、A、F四点共圆;
(2)∵B、C、A、F四点共圆,如图,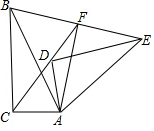
∴∠BFA+∠BCA=180°,
∵∠ACB=90°,
∴∠BFA=90°,
∴AF⊥BE,
∵AB=AE,
∴BF=EF.
点评 本题考查的是四点共圆,需要掌握点与圆的位置关系、圆周角定理以及反证法的应用,掌握反证法的一般步骤、同弧所对的圆周角相等是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某农民带了若干千克玉米进城出卖,为了方便,他带了一些零用钱备用,他先按市场价出卖一些后,又降价卖,卖出玉米千克数x与他手中持有钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题.
某农民带了若干千克玉米进城出卖,为了方便,他带了一些零用钱备用,他先按市场价出卖一些后,又降价卖,卖出玉米千克数x与他手中持有钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com