
【题目】某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,![]() 、
、![]() 是
是![]() 的中线,
的中线,![]() 于点
于点![]() ,像
,像![]() 这样的三角形均称为“中垂三角形”.
这样的三角形均称为“中垂三角形”.
(特例探究)
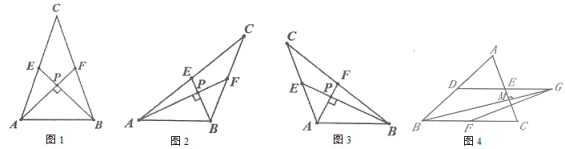
(1)如图1,当![]() ,
,![]() 时,
时,![]() _____,
_____,![]() ______;
______;
如图2,当![]() ,
,![]() 时,
时,![]() _____,
_____,![]() ______;
______;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想![]() 、
、![]() 、
、![]() 三者之间的关系,用等式表示出来,并利用图3证明你的结论;
三者之间的关系,用等式表示出来,并利用图3证明你的结论;
(拓展证明)
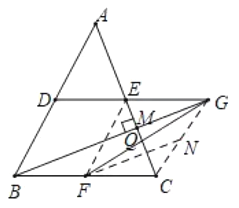
(3)如图4,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]()
![]() 的中点,连结
的中点,连结![]() 并延长至
并延长至![]() ,使得
,使得![]() ,连结
,连结![]() ,当
,当![]() 于点
于点![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() .
.
【解析】
(1)由三角函数的性质得到![]() 根据三角形中位线的性质,得到EF//AB.
根据三角形中位线的性质,得到EF//AB. ![]() ,由平行线分线段成比例可得
,由平行线分线段成比例可得![]() ,可求得PE、PE的长,再由勾股定理得到结果;由三角函数的性质得到
,可求得PE、PE的长,再由勾股定理得到结果;由三角函数的性质得到![]() 根据三角形中位线的性质,得到EF//AB.
根据三角形中位线的性质,得到EF//AB. ![]() ,由平行线分线段成比例可得
,由平行线分线段成比例可得![]() ,可求得PE、PE的长再由勾股定理得到结果;
,可求得PE、PE的长再由勾股定理得到结果;
(2) 设![]() ,
,![]() ,则
,则![]() ,
,![]() ,利用勾股定理用x、y、z分别表示出:
,利用勾股定理用x、y、z分别表示出:![]() 、
、![]() 、
、![]() ,再用x、y、z分别表示出
,再用x、y、z分别表示出![]() ,
,![]() ,由
,由![]() 即可得出答案;
即可得出答案;
(3)连结![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,可得四边形
,可得四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 是中垂三角形,即可知:
是中垂三角形,即可知:![]() ,
,![]() 代入(2)中结论可求得
代入(2)中结论可求得![]()
(1)解:如图,连接EF
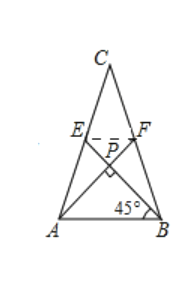
∵![]() ,
,![]() ,
,![]()
∴![]()
∵![]() 、
、![]() 是
是![]() 的中线,
的中线,![]() 是交点
是交点
∴![]()
∴![]()
∴![]()
∵![]()
∴由勾股定理可得:![]()
∴![]()
如图连接EF
∵![]() ,
,![]() ,
,![]()
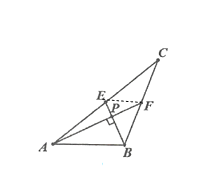
∴![]() ,
,![]()
∵![]() 、
、![]() 是
是![]() 的中线,
的中线,![]() 是交点
是交点
∴![]()
∴![]()
∴![]() ,
,![]()
∵![]()
∴由勾股定理可得:![]() ,
,![]()
∴![]() ,
,![]()
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)![]() ,理由如下:
,理由如下:
设![]() ,
,![]() ,则
,则![]() ,
,![]()
∵![]()
∴![]()
![]()
![]()
∴![]() ,
,
![]()
∴![]()
即![]()
(3)连结![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
∵![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 的中点
的中点
∴![]() 是
是![]() 的中点
的中点
∵![]() ,
,![]() 是
是![]() ,
,![]() 的中点
的中点
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() 是
是![]() 的中点
的中点
∴![]() 是中垂三角形
是中垂三角形
∵![]() ,
,![]() ,
,
∴![]() ,
,![]()
有(2)中结论可知:![]()
∴![]()


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
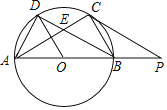
【题目】如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC.
(1)求证:△ADB≌△BCA;
(2)若OD⊥AC,AB=4,求弦AC的长;
(3)在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (b,c为常数).
(b,c为常数).
(1)若抛物线的顶点坐标为(1,1),求b,c的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求c的取值范围;
(3)在(1)的条件下,存在正实数m,n( m<n),当m≤x≤n时,恰好有![]() ,求m,n的值.
,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
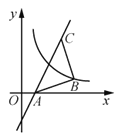
【题目】如图,过点C(3,4)的直线![]() 交
交![]() 轴于点A,∠ABC=90°,AB=CB,曲线
轴于点A,∠ABC=90°,AB=CB,曲线![]() 过点B,将点A沿
过点B,将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,则
个单位长度恰好落在该曲线上,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
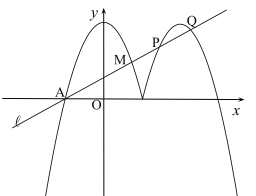
【题目】在平面直角坐标系中,抛物线![]() 的最高点的纵坐标是2.
的最高点的纵坐标是2.
(1)求抛物线的表达式;
(2)将抛物线在![]() 之间的部分记为图象
之间的部分记为图象![]() ,将图象
,将图象![]() 沿直线x=1翻折,翻折后图象记为
沿直线x=1翻折,翻折后图象记为![]() ,图象
,图象![]() 和
和![]() 组成G,直线
组成G,直线![]() :
:![]()
![]() 和图象G在x轴上方的部分有两个公共点,求k的取值范围;
和图象G在x轴上方的部分有两个公共点,求k的取值范围;
(3)直线![]() :
:![]() 与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求
与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com