
【题目】如图,D是等边△ABC的边BC的中点,E、F分别在AB、AC上,∠EDF+∠A=180°,AE:EB=5:1,EF=![]() ,则CF长为__________.
,则CF长为__________.
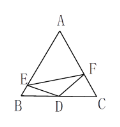
【答案】4
【解析】
取AB的中点M,连接DM,过点E作EN⊥AC,利用三角形中位线定理及AAS定理证得△DEM≌△DFC,从而得到EM=FC,然后设EB=x,结合等边三角形和含30°的直角三角形的性质求得AN=![]() ,EN=
,EN=![]() ,NF=
,NF=![]() ,然后利用勾股定理列方程求解,从而求出CF的长度.
,然后利用勾股定理列方程求解,从而求出CF的长度.
解:取AB的中点M,连接DM
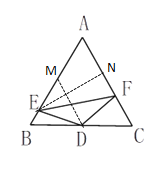
∵∠EDF+∠A=180°
∴在四边形AEDF中,∠AED+∠AFD=180°
又因为∠AFD+∠CFD=180°
∴∠AED=∠CFD
∵D是等边△ABC的边BC的中点,M为AB中点
∴DM∥AC,DM=![]() ,DC
,DC![]() ,AB=AC=BC
,AB=AC=BC
∴∠DMB=∠A=∠C=60°,DM=DC
∴△DEM≌△DFC
∴EM=FC
∵AE:EB=5:1
∴设EB=x,则AE=5x,AB=AC=6x
∴BM=3x,EM=FC=2x,AF=4x
过点E作EN⊥AC
在Rt△AEN中,∠AEN=30°
∴AN=![]() ,则EN=
,则EN=![]() ,NF=
,NF=![]()
∴在Rt△ENF中,![]()
解得:x=±1(负值舍去)
∴CF=4
故答案为:4


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式的化简后,遇到了这样一个需要化简的式子:![]() .该如何化简呢?思考后,他发现
.该如何化简呢?思考后,他发现![]() .于是
.于是![]() .善于思考的小明继续探索:当
.善于思考的小明继续探索:当![]() 时(其中a,b,m,n均为正整数),则
时(其中a,b,m,n均为正整数),则![]() .此时,
.此时,![]() ,
,![]() ,于是,
,于是,![]() .请你仿照小明的方法探索并解决下列问题:
.请你仿照小明的方法探索并解决下列问题:
(1)设a,b,m,n均为正整数且![]() ,用含m,n的式子分别表示a,b时,结果是
,用含m,n的式子分别表示a,b时,结果是![]() _______,
_______,![]() _______;
_______;
(2)若![]() ,
,![]() ,
,![]() ,
,![]() ,……,以此类推,求
,……,以此类推,求![]() 的值.
的值.
(3)若a,b,c分别为△ABC的三条边,且a,b,c满足![]() ,判断△ABC的形状,并说明理由.
,判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 路线运动,到
路线运动,到![]() 点停止;点
点停止;点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,到
运动,到![]() 点停止.若点
点停止.若点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,![]() 秒时点
秒时点![]() 、点
、点![]() 同时改变速度,点
同时改变速度,点![]() 的速度变为每秒
的速度变为每秒![]() ,点
,点![]() 的速度变为每秒
的速度变为每秒![]() .如图
.如图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() (秒)的函数关系图象;图
(秒)的函数关系图象;图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() (秒)的函数关系图象.根据图象:
(秒)的函数关系图象.根据图象:
![]() 求
求![]() 、
、![]() 、
、![]() 的值;
的值;
![]() 设点
设点![]() 出发
出发![]() (秒)后离开点
(秒)后离开点![]() 的路程为
的路程为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式,并求出点
的函数关系式,并求出点![]() 与
与![]() 相遇时
相遇时![]() 的值.
的值.
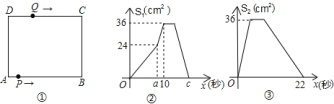
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船航行到 B 处时,测得小岛 A 在船的北偏东 60°的方向,轮船从 B 处继续向正东方向航行 20 海里到达 C 处时,测得小岛 A 在北船的北偏东 30°的方向.
(1)若小岛 A 到这艘轮船航行路线 BC 的距离是 AD,求 AD 的长.
(2)已知在小岛周围 17 海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
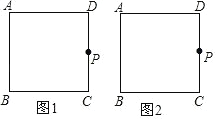
【题目】操作:如图,在正方形 ABCD 中,P 是 CD 上一动点(与 C,D 不重合),使三角板的直角顶点与点 P 重合,并且一条直角边始终经过点 B,另一直角边与正方形的某一边所在直线交于点 E.
(1)根据操作结果,画出符合条件的图形;
(2)观察所画图形,写出一个与△BPC 相似的三角形,并说明理由;
(3)当点 P 位于 CD 的中点时,直接写出(2)中两对相似三角形的相似比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一黄金周”前,某旅行社要印刷旅游宣传材料,甲印刷厂提出:每份材料收1元印刷费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.
(1)分别写出两印刷厂的收费y(元)与印制宣传材料数量x(份)之间的关系式;
(2)旅行社要印制800份宣传材料,选择那家印刷厂比较合算?说明理由.
(3)旅行社拟拿出3000元用于印制宣传材料,哪家印刷厂印制的多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
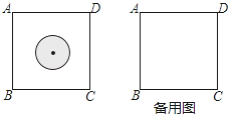
【题目】有一类随机事件概率的计算方法:设试验结果落在某个区域S中的每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率P(A)=![]() . 有一块边长为30cm的正方形ABCD飞镖游戏板,假设飞镖投在游戏板上的每一点的机会均等.求下列事件发生的概率:
. 有一块边长为30cm的正方形ABCD飞镖游戏板,假设飞镖投在游戏板上的每一点的机会均等.求下列事件发生的概率:
(1)在飞镖游戏板上画有半径为5cm的一个圆(如图1),求飞镖落在圆内的概率;
(2)飞镖在游戏板上的落点记为点O,求△OAB为钝角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
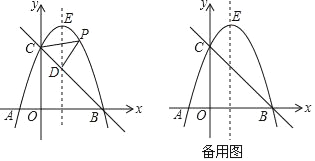
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交A(﹣1,0),B两点,与y轴交于点C(0,3),抛物线的顶点为点E.
(1)求抛物线的解析式;
(2)经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一个动点,当点P运动到点E时,求△PCD的面积;
(3)点N在抛物线对称轴上,点M在x轴上,是否存在这样的点M与点N,使以M,N,C,B为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com