
【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2. 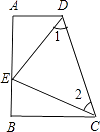
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
【答案】
(1)证明:∵∠1=∠2,
∴DE=CE,
∵在RT△ADE和RT△BEC中, ![]() ,
,
∴RT△ADE≌RT△BEC,(HL)
∴AD=BE,
∵AB=AE+BE,
∴AB=AD+BC
(2)解:∵RT△ADE≌RT△BEC,
∴∠AED=∠BCE,
∵∠BCE+∠CEB=90°,
∴∠CEB+∠AED=90°,
∴∠DEC=90°,
∴△CDE为等腰直角三角形
【解析】(1)易证DE=CE,即可证明RT△ADE≌RT△BEC,可得AD=BE,即可解题;(2)由RT△ADE≌RT△BEC可得∠AED=∠BCE,即可求得∠DEC=90°,即可解题.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+(b﹣2)2=0,则x= ,y= ,并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在用配方法解一元二次方程x2﹣6x=1的过程中配方正确的是( )
A.(x﹣3)2=8B.(x﹣3)2=10C.(x+3)2=1D.(x+3)2=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤![]() .其中正确的个数为( ).
.其中正确的个数为( ).
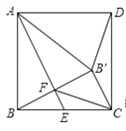
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示. 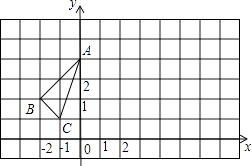
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
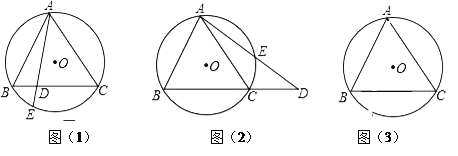
【题目】如图,△ABC内接于⊙O,且AB=AC,
(1)⊙O的弦AE交于BC于D.求证:ABAC=ADAE;
(2)在(1)的条件下当弦AE的延长线与BC的延长线相交于点D时,上述结论是否还成立?若成立,请给予证明.若不成立,请说明理由.
(3)已知⊙O 的半径2,∠ACB=40°,求BA的长.(sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定一种新的运算“*”:对于任意实数x,y,满足x*y=x﹣y+xy.如3*2=3﹣2+3×2=7,则2*1=( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为( )
A.3.7×10﹣5克
B.3.7×10﹣6克
C.37×10﹣7克
D.3.7×10﹣8克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com