
分析 将二次函数配方成顶点式可得最值为-$\frac{5}{4}$a+$\frac{3}{4}$b,根据题意可得-$\frac{a}{2}$=-$\frac{5}{4}$a+$\frac{3}{4}$b即a=b,在顶角∠C=50°的等腰三角形中可求得∠A度数.
解答 解:将二次函数配方得:y=(a+b)(x+$\frac{1}{2}$)2-$\frac{5a}{4}$+$\frac{3b}{4}$,
∵该二次函数的最小值为-$\frac{a}{2}$,
∴-$\frac{a}{2}$=-$\frac{5}{4}$a+$\frac{3}{4}$b,整理,得:a=b,
在△ABC中,
∵∠C=50°,
∴当a=b时,∠A=∠B=$\frac{180°-∠C}{2}$=65°,
故答案为65°.
点评 本题主要考查二次函数的最值,根据解析式配方成顶点式得其最值得表达式是关键,由题意得到等腰三角形根据顶角求底角度数是基础.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:填空题
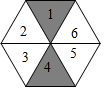 如图所示的六边形广场由若干个大小完全相同的正三角形组成,一只小鸟在广场上随机停留,刚好落在数字是5的三角形区域的概率为$\frac{1}{6}$.
如图所示的六边形广场由若干个大小完全相同的正三角形组成,一只小鸟在广场上随机停留,刚好落在数字是5的三角形区域的概率为$\frac{1}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向下 | B. | 抛物线经过点(3,4) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=-x2+5x+n的图象经过点A(1,0),与y轴交于点B.
如图,二次函数y=-x2+5x+n的图象经过点A(1,0),与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com