

分析 (1)①利用HL定理判定Rt△GBC≌Rt△CPG;
②根据平行四边形的判定定理证明四边形BGCD是平行四边形,得到答案;
(2)证明Rt△GBC≌Rt△GPC,利用正切的定义求出PG的长,根据全等三角形的性质得到答案.
解答 解:(1)①在Rt△GBC和Rt△CPG中,
$\left\{\begin{array}{l}{BC=PG}\\{GC=CG}\end{array}\right.$,
∴Rt△GBC≌Rt△CPG;
②∵Rt△GBC≌Rt△CPG,
∴∠BCG=∠PGC,
∴EG=EC,又BC=PG,
∴EB=EP,
∴∠EBP=∠EPB,
∴∠EBP=∠GCB,
∴BD∥GC,又BG∥CD,
∴四边形BGCD是平行四边形,
∴BG=CD=6;
(2)在Rt△GBC和Rt△GPC中,
$\left\{\begin{array}{l}{BC=PC}\\{GC=GC}\end{array}\right.$,
∴Rt△GBC≌Rt△GPC,
∴PC=BC=8,BG=PG,
∵△GPC是一个三角板,
∴∠PGC=30°,
∴PG=$\frac{PC}{tan30°}$=8$\sqrt{3}$,
∴BG=8$\sqrt{3}$.
点评 本题考查的是矩形的性质、全等三角形的判定和性质、平行四边形的判定,掌握直角三角形全等的判定方法、熟记锐角三角函数的定义是解题的关键.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
| A. | 平均数为6,方差为1 | B. | 平均数为6,方差为4 | ||
| C. | 平均数为8,方差为1 | D. | 平均数为8,方差为4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
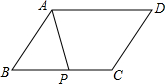 如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,
如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=4,那么点B与C′的距离为( )
如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=4,那么点B与C′的距离为( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com