
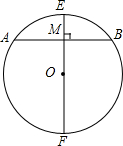
 如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条.
如图所示,M为⊙0内任一不与点O重合的点,连接0M,AB为过M点且与0M垂直的一条弦,EF为过M点的一条直径,求证:在过M点的所有弦中,AB是最短的一条,EF是最长的一条. 科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{x}$ | B. | -$\frac{2}{x}$ | C. | -2x | D. | 2x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
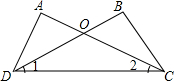 题目:如图,已知AC,BD相交于点0.∠A=∠B,∠1=∠2,试说明△AOD≌△BOC.
题目:如图,已知AC,BD相交于点0.∠A=∠B,∠1=∠2,试说明△AOD≌△BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明家、学校、书店在同-条马路上,请你用学过的数学知识在图中标明它们三者间的距离.小明的步行速度是5千米/时,小明中午11:30放学,下午1:30上课,吃饭要用30分钟,中午他要到书店买完书再到学校上课,选书时间是10分钟.请你帮小明计算一下,他吃完中午饭最晚什么时间从家出发上课才不会迟到?
小明家、学校、书店在同-条马路上,请你用学过的数学知识在图中标明它们三者间的距离.小明的步行速度是5千米/时,小明中午11:30放学,下午1:30上课,吃饭要用30分钟,中午他要到书店买完书再到学校上课,选书时间是10分钟.请你帮小明计算一下,他吃完中午饭最晚什么时间从家出发上课才不会迟到?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
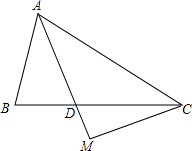 在△ABC中,AD平分∠BAC,且AB=AD,过点C作CM⊥AD交AD延长线于M.
在△ABC中,AD平分∠BAC,且AB=AD,过点C作CM⊥AD交AD延长线于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知在△ABC中,D是BC上一点,$\frac{AB}{AC}=\frac{BD}{DC}$,且AB=7cm,AC=5cm,BC=8cm,求BD和DC的长.
如图所示,已知在△ABC中,D是BC上一点,$\frac{AB}{AC}=\frac{BD}{DC}$,且AB=7cm,AC=5cm,BC=8cm,求BD和DC的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com