
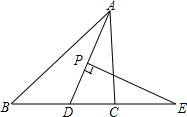
 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E分析 ①中,首先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;
②中,根据第(1)小题的思路即可推导这些角之间的关系.
解答 解:①∵∠B=35°,∠ACB=85°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠DAC=30°,
∴∠ADC=65°,
∴∠E=25°;
②∠E=$\frac{1}{2}$(∠ACB-∠B).
设∠B=n°,∠ACB=m°,
∵AD平分∠BAC,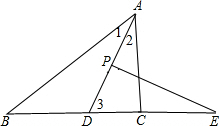
∴∠1=∠2=$\frac{1}{2}$∠BAC,
∵∠B+∠ACB+∠BAC=180°,
∵∠B=n°,∠ACB=m°,
∴∠CAB=(180-n-m)°,
∴∠BAD=$\frac{1}{2}$(180-n-m)°,
∴∠3=∠B+∠1=n°+$\frac{1}{2}$(180-n-m)°=90°+$\frac{1}{2}$n°-$\frac{1}{2}$m°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-(90°+$\frac{1}{2}$n°-$\frac{1}{2}$m°)=$\frac{1}{2}$(m-n)°=$\frac{1}{2}$(∠ACB-∠B).
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
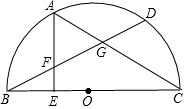 已知:如图,BC是半⊙O的直径,点D在半⊙O,上点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G.
已知:如图,BC是半⊙O的直径,点D在半⊙O,上点A是弧BD的中点.AE⊥BC,垂足为E,BD分别交AE,AC于点F,G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-$\frac{1}{3}$|和-$\frac{1}{3}$ | B. | |-$\frac{1}{3}$|和-3 | C. | |-$\frac{1}{3}$|和$\frac{1}{3}$ | D. | |-$\frac{1}{3}$|和3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com