
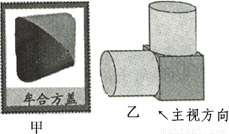
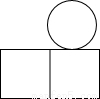
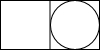
 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是
我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是



科目:初中数学 来源: 题型:
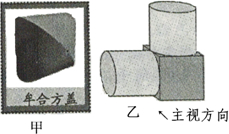 (2012•温州)我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
(2012•温州)我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省生学业考试数学试卷(解析版) 题型:选择题
我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )。
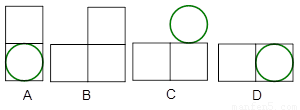
查看答案和解析>>
科目:初中数学 来源:2013年山东省淄博市中考数学模拟试卷(解析版) 题型:选择题
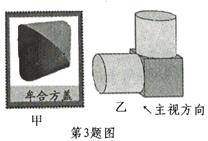
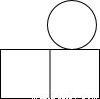
 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )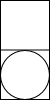

查看答案和解析>>
科目:初中数学 来源:2013年河北省廊坊市大城县中考数学模拟试卷(3月份)(解析版) 题型:选择题
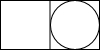
 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )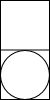

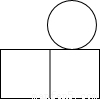
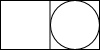
查看答案和解析>>
科目:初中数学 来源:2012年浙江省温州市中考数学试卷(解析版) 题型:选择题
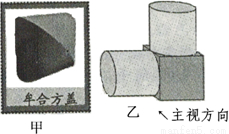 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )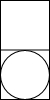

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com