
 如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )
如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )| A. | -3、$-\frac{1}{2}$、1 | B. | $-\frac{1}{2}$、-3、1 | C. | 1、-3、$-\frac{1}{2}$ | D. | -3、1、$-\frac{1}{2}$ |
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:选择题
| A. | 在一个三角形中最多有两个锐角 | B. | 在一个三角形中最多有两个钝角 | ||
| C. | 在一个三角形中最多有两个直角 | D. | 在一个三角形中最少有两个锐角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
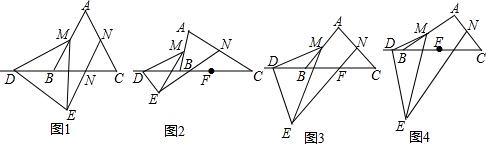
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
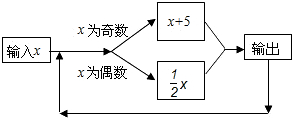 按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第2次得到的结果为12,…,请你探索第2013次得到的结果是( )
按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第2次得到的结果为12,…,请你探索第2013次得到的结果是( )| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
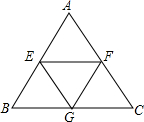 如图,E、F、G分别为等边△ABC的边AB,AC,BC的中点,在以A、B、C、E、F、G为起点或终点的向量中,求出与$\overrightarrow{EF}$平行的向量.
如图,E、F、G分别为等边△ABC的边AB,AC,BC的中点,在以A、B、C、E、F、G为起点或终点的向量中,求出与$\overrightarrow{EF}$平行的向量.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
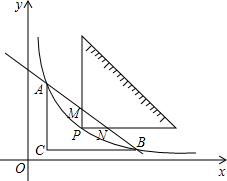 如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+b与双曲线y=$\frac{4}{x}$的交点.
如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+b与双曲线y=$\frac{4}{x}$的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com