
����Ŀ����֪��ͼ����COD=90�㣬ֱ��AB��OC���ڵ�B����OD���ڵ�A������OE������AF���ڵ�G��
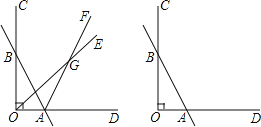
��1����OEƽ����BOA��AFƽ����BAD����OBA=30�㣬����OGA=
��2������GOA=![]() ��BOA����GAD=
��BOA����GAD=![]() ��BAD����OBA=30�㣬����OGA=
��BAD����OBA=30�㣬����OGA=
��3������2���С���OBA=30�㡱��Ϊ����OBA=�����������������䣬����OGA= ![]() �� ���ú����Ĵ���ʽ��ʾ��
�� ���ú����Ĵ���ʽ��ʾ��
��4����OE����BOA�ֳ�1��2�����֣�AFƽ����BAD����ABO=����30��������90�㣩������OGA�Ķ������ú����Ĵ���ʽ��ʾ��
���𰸡���1��15�㣻
��2��10�㣻
��3��![]() ��
��
��4����OGA�Ķ���Ϊ![]() ��+15���
��+15���![]() ����15��
����15��
��������
�����������1��������BAD=��ABO+��BOA=��+90�㣬��AFƽ����BAD�õ���FAD=![]() ��BAD������FAD=��EOD+��OGA��2��45��+2��OGA=��+90�㣬����OGA=
��BAD������FAD=��EOD+��OGA��2��45��+2��OGA=��+90�㣬����OGA=![]() ����Ȼ��Ѧ�=30�������㼴�ɣ�
����Ȼ��Ѧ�=30�������㼴�ɣ�
��2��������GOA=![]() ��BOA=30�㣬��GAD=
��BOA=30�㣬��GAD=![]() ��BAD����OBA=����������FAD=��EOD+��OGA�õ�3��30��+3��OGA=��+90�㣬����OGA=
��BAD����OBA=����������FAD=��EOD+��OGA�õ�3��30��+3��OGA=��+90�㣬����OGA=![]() ����Ȼ��Ѧ�=30�������㣻
����Ȼ��Ѧ�=30�������㣻
��3���ɣ�2���õ���OGA=![]() ����
����
��4�����ۣ�����EOD����COE=1��2ʱ��������BAD=��ABO+��BOA=��+90�㣬��FAD=��EOD+��OGA�õ�2��30��+2��OGA=��+90�㣬����OGA=![]() ��+15�㣻
��+15�㣻
����EOD����COE=2��1ʱ������EOD=60�㣬ͬ������OGA=![]() ����15�㣮
����15�㣮
�⣺��1��15�㣻
��2��10�㣻
��3��![]() ��
��
��4������EOD����COE=1��2ʱ��
����EOD=30�㣬
�ߡ�BAD=��ABO+��BOA=��+90�㣬
��AFƽ����BAD��
���FAD=![]() ��BAD��
��BAD��
�ߡ�FAD=��EOD+��OGA��
��2��30��+2��OGA=��+90�㣬
���OGA=![]() ��+15�㣻
��+15�㣻
����EOD����COE=2��1ʱ������EOD=60�㣬
ͬ���õ���OGA=![]() ����15�㣬
����15�㣬
����OGA�Ķ���Ϊ![]() ��+15���
��+15���![]() ����15�㣮
����15�㣮
�ʴ�Ϊ15�㣬10�㣬![]() ����
����


 �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ���ڵ�������A��1��3����B��4��1����O��0��0��������ABO�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������l�ϣ�һ����Q��ԭ��O��������ֱ��l��ÿ����2����λ���ȵ��ٶ������ƶ������ƶ���ʽ���������ƶ�1����λ���ȣ��������ƶ�2����λ���ȣ��������ƶ�3����λ���ȣ��������ƶ�4����λ���ȣ��������ƶ�5����λ���ȡ�
![]()
��1�����5���Ӻ�Q������λ�ã�
��2�����������l�ϻ���һ������A����A��ԭ��O���20����λ���ȣ��ʣ�����Q��ԭ��������������A�غ������ܣ����һ�����A�غ���ʱ�䣿�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʽ��x+6��0=1�����������ǣ�������
A. xΪ������ B. x��0 C. x��6 D. x�٩�6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E��F�ǶԽ���BD�ϵ����㣬��BE��DF.
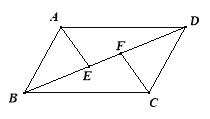
��֤����1����ABE�ա�CDF����2��AE��CF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ ����ABC�ǵ���ֱ�������Σ���A=90������P��Q�ֱ���AB��AC�ϵĶ��㣬������BP=AQ��D��BC���е���
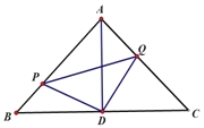
��1����֤����PDQ�ǵ���ֱ�������Σ�
��2������P�˶���ʲôλ��ʱ���ı��Σ�PDQ�������Σ�˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶����ʵ��С���ѧ����ÿ����Ұ���20��ѧ������ȱ��3����ң���ÿ����Ұ���24��ѧ������ճ�һ����ң�������ѧУ���н��Ҷ��ټ䣿
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com