
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
 为了美化环境,某学校在教学楼前铺设小广场地面,其图案如图所示,正方形小广场地面的边长是40米.中心建一个直径为正方形边长一半的圆形花坛,四个角各留一个边长为正方形小广场的四分之一的小正方形花坛,种植高大的树木.图中阴影郁分铺设广场砖.
为了美化环境,某学校在教学楼前铺设小广场地面,其图案如图所示,正方形小广场地面的边长是40米.中心建一个直径为正方形边长一半的圆形花坛,四个角各留一个边长为正方形小广场的四分之一的小正方形花坛,种植高大的树木.图中阴影郁分铺设广场砖.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
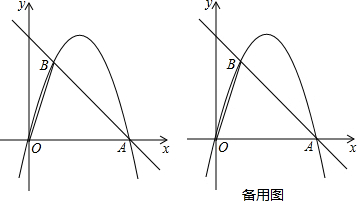
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
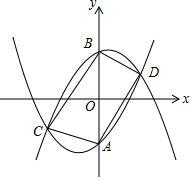 在平面直角坐标系中,我们把关于原点对称的两条抛物线叫做“哥俩好”抛物线.
在平面直角坐标系中,我们把关于原点对称的两条抛物线叫做“哥俩好”抛物线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
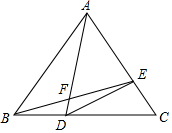 如图,△ABC是等边三角形,点D从点B出发沿BC向点C运动,点E以相同的速度从点C出发沿CA向点A运动,BE与AD相交于点F,连结DE.则下列结论:①若BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,则DE⊥AC;②CE2=DF•DA;③AF•BE=AE•AC;④若△ABC的边长为2$\sqrt{3}$,点F随点D、E运动,则点F运动所经过的路径长为4π,其中正确的有①②③(填序号)
如图,△ABC是等边三角形,点D从点B出发沿BC向点C运动,点E以相同的速度从点C出发沿CA向点A运动,BE与AD相交于点F,连结DE.则下列结论:①若BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,则DE⊥AC;②CE2=DF•DA;③AF•BE=AE•AC;④若△ABC的边长为2$\sqrt{3}$,点F随点D、E运动,则点F运动所经过的路径长为4π,其中正确的有①②③(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com