练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，是用棋子摆成的“上”字：如果按照此规律继续摆下去，那么通过观察，可以发现：第10个“上”字需用多少枚棋子（　　）
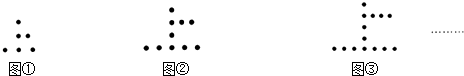
    A．36B．38C．42D．50

    分析 由图可得，第1个“上”字中的棋子个数是6；第2个“上”字中的棋子个数是10；第3个“上”字中的棋子个数是14；…进一步发现规律：第n个“上”字中的棋子个数是（4n+2）；由此求得问题答案．

    解答 解：第1个“上”字中的棋子个数是6=4+2；
    第2个“上”字中的棋子个数是10=4×2+2；
    第3个“上”字中的棋子个数是14=4×3+2；
    …
    第n个“上”字中的棋子个数是（4n+2）；
    所以第10个“上”字需用棋子的数量是4×10+2=42个．
    故选：C．

    点评 本题主要考查了图形的变化规律，对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．通过分析找到各部分的变化规律后直接利用规律求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．在日历上，我们发现某些数会满足一定的規律，比如2016年1月份的日历，我们设计这样的算法：任意选择其中的2×2方框，将方框中4个位置上的数先平方，然后交叉求和，再相减 请你按照这个算法完成下列计算，并回答以下问题
    [2016年1月份的日历]
    日一二三四五六
    12
    3456789
    10111213141516
    17181920212223
    24252627282930
    31
    （1）计算：（12+92）-（22+82）=14，（102+182）-（112+172）=14，自己任选一个有4个数的方框进行计算14
    （2）通过计算你发现什么规律，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．（2x-y）2=4x2-4xy+y2，（-$\frac{1}{4}$a-$\frac{2}{3}$b）2=$\frac{1}{16}$a2+$\frac{1}{3}$ab+$\frac{4}{9}$b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．观察下列各式，解答问题：
    第1个等式：22-12=2×1+1=3；
    第2个等式：32-22=2×2+1=5；
    第3个等式：42-32=2×3+1=7；
    第4个等式：52-42=2×4+1；
    …
    第n个等式：（n+1）2-n2=2n+1．（n为整数，且n≥1）
    （1）根据以上规律，在上边横线上写出第4个等式和第n个等式，并说明第n个等式成立；
    （2）请从下面的A，B两题中任选一道题解答，我选择A或B题．
    A．利用以上规律，计算20012-20002的值．
    B．利用以上规律，求3+5+7+…+1999的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．先化简，再求值：（5x-y）（2x+y）-（3y+2x）（3y-2x），其中x=1，y=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，下列图形中的数字按一定规律排列，按此规律，则第6个图中m的值为（　　）
    A．$\frac{3}{8}$B．$\frac{7}{36}$C．$\frac{11}{48}$D．$\frac{13}{96}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．课题学习
    问题背景1  甲、乙、丙三名同学探索课本上一道题：如图1，E是边长为a的正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，
    （1）①在图中画出旋转后的图形；
    ②图1中，与线段AE垂直的线段是AK⊥AE，说明你的理由．
    问题背景2  如图2，在正方形ABCD中，∠EAF=45°，点F为BC上一点，点E为DC上一点，∠EAF的两边AE、AF分别与直线BD交于点M、N，连接EF，继续探索时，甲认为：线段BF、EF和DE之间存在着关系式EF=BF+DE；乙认为△CEF的周长是一个恒定不变的值；丙认为：线段BN、MN和DM之间存在着关系式BN2+DM2=MN2
    （2）请你对甲、乙、丙三人中一个结论进行研究，作出判断，并说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知A=$\frac{1}{2}$x2-x+5，B=3x-1+x2，当x=-2时，求A-2B．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

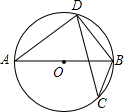    10．如图，AB是⊙O的直径，CD是⊙O的弦，连接AD、DB、BC，若∠ABD=55°，则∠BCD的度数为（　　）
    A．65°B．55°C．45°D．35°

    查看答案和解析>>

    同步练习册答案