练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，是边长为的等边三角形，其中是坐标原点，顶点在轴的正方向上，将折叠，使点落在边上，记为′，折痕为。

    (1）当轴时，求点′和的坐标；

    (2）当轴，且抛物线经过点′和时，求该抛物

    　　　　 线与轴的交点的坐标；

    (3）当点′在上运动但不与点、重合时，能否使成为直角

    　　　　 三角形？若能，请求出此时点′的坐标；若不能，请你说明理由。
    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

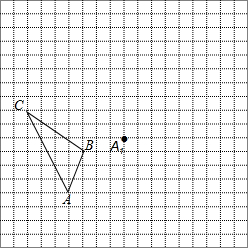    （2012•安徽）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点A1．
    （1）画出一个格点△A1B1C1，并使它与△ABC全等且A与A1是对应点；
    （2）画出点B关于直线AC的对称点D，并指出AD可以看作由AB绕A点经过怎样的旋转而得到的．

    查看答案和解析>>

    科目：初中数学 来源：鼎尖助学系列—同步练习(数学 九年级下册)、期末测试题 题型：044

    如图△OAB是边长为的等边三角形，其中O是坐标原点，顶点B在y轴的正方向上，将△OAB折叠，使点A落在边OB上，记为A′，折痕为EF．

    (1)

    当A′E∥x轴时，求点A′和E的坐标；

    (2)

    当A′E∥x轴时，且抛物线经过点A′和A时，求该抛物线与x轴的交点坐标；

    (3)

    当点A′在OB上运动但不与点O、B重合时，能否使△A′EF成为直角三角形？若能，请求出此时点A′的坐标；若不能，请你说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年江苏省江阴市顾山九年级上学期期末考试数学试卷（解析版） 题型：解答题

    阅读下面材料：

    小明遇到这样一个问题：如图1,在边长为的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现：分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形（如图2）

    请回答：

    （1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙,不重叠）,则这个新的正方形的边长为__________；

    （2）求正方形MNPQ的面积.

    参考小明思考问题的方法,解决问题：

    如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若,则AD的长为__________.

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

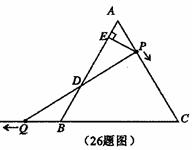
    如图，△是边长为6的等边三角形， 是边上一动点，由向运动（与、不重合），是延长线上一动点，与点同时以相同的速度由向延长线方向运动（不与重合），过作⊥于，连接交于.

    （1）当∠时，求的长；

    （2）在运动过程中线段的长是否发生变化？如果不变，求出线段的长；如果发生改变，请说明理由．

    查看答案和解析>>

    同步练习册答案