
| A. | ①② | B. | ② | C. | ③ | D. | ②③ |
分析 ①求出方程的两个实数根进行判断即可;
②根据根与系数的关系进行判断即可;
③由方程ax2+bx+c=0是倍根方程,得到x1=3x2,由相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,通过抛物线对称轴求得x1的值
解答 解:①解方程x2-4x-12=0得,x1=-2,x2=6,
∵6≠3×(-2),
∴此方程不是立根方程,故①错误;
②∵点(p,q)在反比例函数y=$\frac{3}{x}$的图象上,
∴pq=3.
∴方程px2+4x+q=0中,x1•x2=$\frac{q}{p}$=3,
∴关于x的方程px2+4x+q=0是立根方程,故②正确;
③∵方程ax2+bx+c=0是立根方程,
∴设x1=3x2,
∵相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,
∴抛物线的对称轴x=$\frac{1+t+4-t}{2}$=$\frac{5}{2}$,
∴x1+x2=5,
∴x1+3x1=5,
∴x1=$\frac{5}{4}$,
故③正确.
综上所述,正确的个数是2个.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
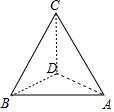 如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量.在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处侧得塔顶C在东偏北40°的方向上,仰角为30°,若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$m.
如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量.在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处侧得塔顶C在东偏北40°的方向上,仰角为30°,若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
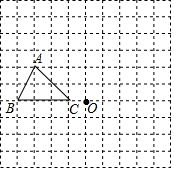 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC顶点都在格点上(每个小方格的顶点叫格点).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(±3)^{2}}$=±3 | B. | 23×24=27 | C. | -2a2•3a=6a3 | D. | 3m2÷(3m-1)=m-3m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com